AlphaBlend, AlphaTest, AlphaSort

Alpha blending, Alpha test, Alpha sorting

Alpha blending

알파 블렌딩은 각 픽셀에 투명도 값 (알파채널)을 적용하여 두 개 이상의 이미지를 결합하는 프로세스를 말합니다. 이렇게 하면 이미지가 부분적으로 겹쳐져 매끄러운 블렌딩을 만들 수 있습니다.

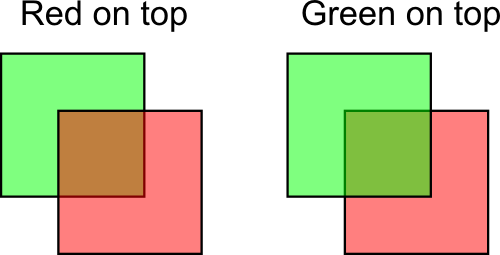
다음은 알파 블렌딩이 일반적으로 사용되는 몇 가지 상황입니다:

1. 겹치는 개체: 투명한 물체를 겹쳐서 겹치는 것과 같은 복잡한 합성 효과를 만들 수 있습니다.
2. 시뮬레이션 : 연기 불 물과 같은 사실적인 시뮬레이션에 필수적.

다음은 단계별 분석입니다:
투명도가 있는 이미지를 렌더링할 때 컴퓨터는 덧셈 프로세스를 사용하여 두 이미지의 픽셀을 결합합니다.

1. 소스 알파: 각 소스 픽셀에는 투명 또는 불투명 정도를 나타내는 알파 채널(0~255)이 연관되어 있습니다.
2. 대상 알파: 마찬가지로 대상 픽셀에도 자체 알파 채널이 있습니다.
3. 픽셀 조합: 컴퓨터는 각 소스 픽셀의 색상 및 불투명도 값에 해당 대상 픽셀의 색상 및 불투명도 값을 곱하여 두 이미지를 결합합니다.

알파 블렌딩을 사용하는 이유는 무엇인가요?

1. 사실적인 합성: 알파 블렌딩을 사용하면 투명도를 정밀하게 제어하여 겹치는 요소가 자연스럽게 보이도록 할 수 있습니다.
2. 효율적인 렌더링: 알파 블렌딩은 애디티브 프로세스를 사용하여 전체 장면을 여러 번 렌더링하거나 복잡한 조명 효과를 다시 계산할 필요성을 줄여줍니다.

알파 블렌딩의 옵션

• 덧셈 블렌딩(색상을 함께 추가)
• 감산 혼합(한 색상에서 다른 색상 빼기)
• 곱하기 블렌딩(색상을 함께 곱함)

// AlphaBlendShader.hlsl

float4 main(float2 uv : TEXCOORD0, float4 color : COLOR) : SV_Target
{
    // UV 좌표에서 텍스처 샘플
    float4 texColor = tex2D(TextureSampler, uv);

    // 샘플링된 텍스처에서 알파 값 계산하기
    float alpha = texColor.a;

    // 텍스처의 알파 값과 입력 색상을 혼합합니다.
    return lerp(color, color * alpha, alpha);
}

---

Alpha sorting

알파 정렬은 알파 채널에 따라 오브젝트를 정렬하는 데 사용되는 알고리즘입니다. 불투명 개체를 우선적으로 그리고 이를 통해 투명한 오브젝트가 올바른 순서로 올바르게 렌더링 되도록 할 수 있습니다. 알파 블렌딩과 함께 작동하여 투명한 요소가 올바르게 렌더링 되도록 합니다.

알파 정렬을 사용하는 이유:

• 투명도에 따라 오브젝트를 정렬하여 Z-파이팅(두 개 이상의 겹치는 오브젝트의 깊이가 비슷한 경우)을 방지합니다.
• 알파 값에 따라 정렬해야 하는 사실적인 시뮬레이션을 제작할 때 매우 중요합니다.

두 개의 투명 오브젝트의 순서가 같고(즉, 둘 다 동시에 그려짐) 위치가 동일하면(즉, 정확히 동일한 픽셀 좌표를 차지함) Z-파이팅으로 알려진 시각적 아티팩트가 발생할 수 있습니다. 이 문제를 해결하려면 이러한 개체가 깊이 측면에서 겹치지 않도록 해야 합니다.

1. 깊이 정렬: 렌더링하기 전에 투명 오브젝트를 깊이별로 정렬합니다. 이렇게 하면 가까운 오브젝트가 먼 오브젝트 위에 그려집니다.

2. Z 버퍼링을 사용한 알파 블렌딩: (애디티브 블렌딩이라고도 함)을 사용하고 z-버퍼가 겹치는 픽셀을 올바르게 처리할 수 있도록 설정합니다.

3. 깊이 필링 사용: 개체의 깊이가 다양한 경우 ‘뎁스 필링’이라는 기술을 사용하여 카메라로부터의 거리에 따라 레이어로 렌더링합니다.
4. 사전 렌더링: 투명 오브젝트를 다양한 거리에 미리 렌더링하여 텍스처 또는 스프라이트로 저장합니다. 그런 다음 렌더링할 때 각 픽셀에 대해 올바른 사전 렌더링된 오브젝트를 선택하기만 하면 됩니다.

---

Alpha test

알파 테스트는 개체의 픽셀이 완전히 불투명한지 또는 투명한지를 결정하는 데 사용되는 기법입니다. 렌더링 엔진이 먼저 렌더링할 개체를 결정하고 투명도 효과가 올바르게 나타나는지 확인하는 데 도움이 됩니다.

작동 방식은 다음과 같습니다:

1. 픽셀 비교: 렌더러는 장면의 각 픽셀을 해당 알파 값(0-255)과 비교합니다. 알파 값이 0이면 픽셀은 완전히 투명합니다.
2. 알파 임계치: 픽셀을 불투명하게 간주할지 여부를 결정하기 위해 미리 정의된 임계값이 설정됩니다. 일반적으로 이 임계값은 약 128(0과 255의 중간값)입니다.
3. 픽셀 분류:

• 알파 값이 임계값보다 낮으면 픽셀이 투명으로 분류됩니다.
• 알파 값이 임계값 이상이면 픽셀이 불투명하게 간주됩니다.

알파 테스트는 렌더링을 최적화 합니다.

1. 오버드로우 감소: 렌더러는 파이프라인 초기에 완전히 불투명한 픽셀을 식별하여 가려질 수 있는 후속 레이어나 오브젝트의 렌더링을 건너뛸 수 있습니다.
2. 성능 개선: 알파 테스트는 렌더링 및 처리할 픽셀 수를 줄여 프레임 속도가 빨라집니다.

// AlphaTestShader.hlsl

float4 main(float2 uv : TEXCOORD0, float4 color : COLOR) : SV_Target
{
    // UV 좌표에서 텍스처 샘플
    float4 texColor = tex2D(TextureSampler, uv);

    // 샘플링된 텍스처에서 알파값을 계산합니다.
    float alpha = texColor.a;

    // 픽셀의 알파 값이 특정 임계값보다 큰지 테스트합니다
    if (alpha > 0.5f) {
        return color;
    } else {
        clip; // 픽셀이 잘려서 렌더링되지 않음
    }
}

아래에서는 각 상황을 케이스로 분류하여 분석합니다.

1. Transparency 는 T, Opaque는 O로 표기합니다.
2. 각 개체는 카메라 기준점으로 부터 거리가 N(near), F(far)로 표기됩니다.
3. Opaque는 render queue에 의해 T 개체보다 먼저 그려집니다.

Case 1 T(가까이) + O(멀리)

• 렌더링 순서 : O가 먼저 그려집니다
• 알파 블렌딩 : T는 O 다음에 렌더링 되므로 이전에 렌더링 된 O 위에 색상 값이 블렌딩 됩니다. 즉, T의 투명한 픽셀 중 일부분이 O의 색상을 덮어쓰게 됩니다.

예시 : T(50 % 알파)->O 결과 : O의 색이 T의 색으로 덮어 씌워집니다.

Case 2 O(가까이) + T(멀리)

• 렌더링 순서 : O가 먼저 그려집니다.
• 알파 블렌딩 : T는 O 보다 먼 곳에 렌더링 되므로 O에 의해 가려지게 됩니다.

예시 :O->T(50 % 알파) 결과 : 불투명 개체의 색이 투명 개체의 색으로 덮어 씌워집니다.

Case 3 두 개의 T, 하나는 Near 하나는 Far

• 렌더링 순서 : Alpah sorting으로 정렬된 개체 중 가장 먼 개체를 우선적으로 렌더링 합니다. 이후 먼 곳에서 가까운 곳으로 순차적으로 렌더링 됩니다.

• 알파 블렌딩 : 두 개체 모두 투명하므로 색상 값이 이전 렌더링 된 결과값과 블렌딩됩니다. 결과 알파 값은 두 개체의 투명도를 고려합니다.

투명 개체 렌더링시 순서가 반대로 렌더링 되는것은 3D 그래픽에서 원근 투영이 작동하는 방식 때문입니다. Z 버퍼링과 뎁스 테스트가 함께 작동하는 방식 때문에 카메라에 가까운 오브젝트는 멀리 있는 오브젝트보다 늦게 렌더링됩니다.

예시: TransparentObject1 (50% 알파) -> TransparentObject2 (30% 알파)
결과 : 최종 알파 값은 원래 알파 값에 곱하고 색상 값과 혼합하여 계산됩니다. 이 경우 결과는 15% 투명 개체(0.5 * 0.3)가 됩니다.

---

Z -buffer

Z 버퍼(깊이 버퍼라고도 함)는 카메라로부터의 거리를 기준으로 오브젝트를 정렬하는 데 사용되는 기법입니다. 이를 통해 투명 또는 반투명 오브젝트의 올바른 렌더링 순서를 보장할 수 있습니다.

Depth Test

깊이 테스트는 각 픽셀의 계산된 깊이 값을 Z 버퍼에 저장된 깊이 값과 비교하는 프로세스입니다. 이를 통해 픽셀을 렌더링할지 아니면 폐기할지 여부를 결정합니다.

Z buffer가 어떻게 렌더 순서를 보장하는가?

계산된 깊이 값?

픽셀 위치를 기준으로 각 픽셀이 카메라로부터 떨어진 거리를 나타냅니다.

저장된 깊이 값?

이전에 다른 픽셀이나 오브젝트에 의해 z-버퍼에 기록된 카메라로부터의 거리입니다.

이후 래스터화 과정중 계산된 깊이 값과 z 버퍼에 저장된 깊이 값을 비교하여 계산 결과가 z 버퍼에 기록된 값보다 카메라에 가까우면 z 버퍼에 기록하고 렌더를 수행합니다.

아닐경우 (더 가까운 오브젝트가 이미 렌더 되었을 때) 픽셀을 폐기합니다. 해당 과정을 depth buffering 또는 z buffering이라고 합니다.

float CalculatedValue;
float StoredValueZbuffer;

if(CalculatedValue > StoredValueZbuffer)
	// 계산된 깊이 값이 카메라로부터 멀게되므로 픽셀을 그리지 않습니다.
else if(CalculatedValue < StoredValueZbuffer)
	// 계산된 깊이 값이 카메라로부터 가까우므로 렌더를 진행합니다.

작동 방식은 다음과 같습니다

1. 심도 계산: 각 픽셀은 카메라로부터의 거리를 나타내는 자체 깊이 값을 계산합니다.
2. Z-버퍼 저장: 렌더러는 이러한 깊이 값을 버퍼( 16비트 또는 32비트 부동소수점)에 저장합니다.
3. 소팅 및 렌더링: 객체가 렌더링될 때:
   • 렌더러는 현재 픽셀의 깊이가 Z 버퍼에 저장된 값과 일치하는지 확인합니다.
   • 일치하면 픽셀은 카메라에서 더 멀리 떨어져 있는 다른 객체(즉, 다른 객체 뒤)에 의해 가려진 것으로 간주합니다. 이 경우 렌더러는 해당 픽셀의 렌더링을 건너뛰거나 알파 블렌딩을 사용하여 여러 레이어를 결합합니다.
   • 그렇지 않으면 픽셀이 평소처럼 렌더링됩니다.

Z - buffer의 이점

1. 오버드로우 줄이기: 렌더러는 깊이를 기준으로 오브젝트를 정렬하여 다른 오브젝트에 가려진 픽셀을 렌더링하는 것을 건너뛸 수 있습니다.

2. 성능 향상: Z-버퍼링은 렌더링 및 처리할 픽셀 수를 줄여 프레임 속도를 높입니다.

---

Can Z buffer use for Transparency?

반면 Transparency 개체를 렌더할 때는 블렌딩 조건에 의해 Z buffer를 쓸 수 없습니다. (작동하지 않는다는 것은 아닙니다) 아래와 같은 이유로 알파 소팅, 알파 테스팅 등의 추가적인 기술을 필요로 합니다.

• 카메라와의 거리가 고정되어 있지 않기에 동작하지 않습니다.

• 뎁스 버퍼링: 투명 오브젝트의 불투명도는 배경이 얼마나 보이는지에 영향을 미치기 때문에 렌더러는 단순히 투명 오브젝트의 뎁스 버퍼 값을 계산할 수 없습니다.

• 블렌딩: 렌더링 엔진은 투명도를 올바르게 처리하기 위해 블렌딩 공식을 사용하여 겹치는 픽셀의 색상을 결합합니다(예: 반투명 오브젝트가 다른 오브젝트와 겹치는 경우).

• 순서 독립적 정렬 (OIT): 투명 오브젝트는 렌더러가 깊이 버퍼 값에 따라 어떤 오브젝트를 먼저 렌더링할지 결정하는 순서 독립적 정렬이 필요한 경우가 많습니다

이러한 Transparency 개체에 대한 예외와 최적화가 있습니다.

1. 일부 엔진은 다른 정렬 알고리즘을 사용할 수 있습니다: 렌더링 패스 수를 줄이기 위해 토폴로지 정렬 또는 공간 파티셔닝과 같은 알고리즘을 사용할 수 있습니다.
2. 스텐실 버퍼 또는 오클루전 쿼리를 사용하는 경우 성능상의 이유로 렌더링 순서를 반대로(근거리에서 원거리로) 변경할 수 있습니다.

---

situation 1 물체간 관통시 경계면 처리

1. 여러 오브젝트가 서로 교차하는 경우 공간 분할이라는 기술을 사용하여 경계를 분류해야 합니다. 여기에는 장면을 더 작은 영역으로 나눈 다음 해당 영역 내에 어떤 오브젝트가 있는지 확인하는 작업이 포함됩니다.
   한 가지 일반적인 방법은 각 노드가 3D 공간의 영역을 나타내는 옥트리(나무와 같은 데이터 구조)를 사용하는 것입니다. 두 개체가 교차하면 같은 노드에 속하는지 여부를 확인합니다.

   뎁스 버퍼의 경우 깊이가 다른 여러 개체를 렌더링할 때 GPU는 깊이 버퍼를 사용하여 카메라에 더 가까운 개체를 결정하고 이를 먼저 렌더링합니다.
   불투명한 물체(빛이 통과하지 못하는 물체)가 투명한 물체와 교차하는 경우 이 상황을 신중하게 처리해야 합니다. 알파 블렌딩이나 오클루전 컬링과 같은 기술을 사용하여 적절한 렌더링을 보장할 수 있습니다.

situation 2 불투명, 투명 개체간의 관통

1. 교차 불투명 오브젝트가 포함된 경우 깊이 버퍼 값의 순서대로 렌더링하기만 하면 됩니다.
   유리나 물과 같은 투명 오브젝트의 경우 빛이 이러한 오브젝트를 통과하여 장면의 다른 요소와 상호작용하기 때문에 상황이 더 복잡해집니다. 정확한 렌더링을 위해서는 알파 블렌딩, 애디티브 블렌딩 또는 레이 트레이싱과 같은 기술을 사용해야 합니다.

situation 3 오브젝트간 소팅이 어떻게 이루어지는가?

1. 유니티와 언리얼 같은 엔진은 다양한 알고리즘과 데이터 구조를 사용하여 내부적으로 오브젝트 소팅을 처리합니다.
   유니티에서는 공간 분할(옥트리)과 바운딩 볼륨(구체 또는 박스 등)을 조합하여 카메라의 뷰 프러스텀에 표시되는 오브젝트를 빠르게 결정할 수 있습니다.

   언리얼 엔진은 자체 렌더링 파이프라인에서 비슷한 접근 방식을 사용합니다. 또한 오클루전 컬링 및 레벨 오브 디테일(LOD) 같은 기술을 사용하여 성능을 최적화합니다.

---

부록

Z-fighting이란 무엇인가요?
컴퓨터 그래픽에서는 비슷한 깊이를 가진 두 개 이상의 객체가 동일한 픽셀 위치에서 렌더될 때 Z-fighting(깊이 버퍼 정밀도 문제라고도 함)이 발생합니다. 이는 깊이 값을 계산하는 데 사용되는 부동 소수점 연산의 제한으로 인해 발생할 수 있습니다.

이 경우 렌더러가 한 객체를 다른 객체 위에 렌더링하여 다음과 같은 시각적 아티팩트가 발생할 수 있습니다:

• 깜박임
• 얼룩말 모양의 패턴(두 개체 사이를 번갈아 가며 표시)
• 잘못된 렌더링 순서

CG에서 Z-fighting은 언제 발생했나요?
Z-fighting은 컴퓨터 그래픽 초기부터 문제가 되어왔습니다. 특히 1990년대 후반과 2000년대 초반 3D 그래픽 붐이 일었을 때 많은 게임과 애플리케이션에서 깊이 계산에 고정 소수점 또는 저정밀 부동 소수점 연산을 사용했을 때 널리 퍼졌습니다.

투명성에서 Z-fighting이 발생할 수 있나요?
투명도는 Z-파이팅 문제를 악화시킬 수 있습니다. 투명한 개체가 서로 겹치는 경우 개체의 위치, 크기 및 재질 속성(예: 알파 블렌딩) 간의 복잡한 상호 작용으로 인해 깊이를 정확하게 계산하기 어려울 수 있습니다.

두 개 이상의 반투명 오브젝트가 동일한 픽셀 위치에 비슷한 깊이로 렌더링되는 경우 고정밀 부동 소수점 연산을 사용하는 경우에도 Z-파이팅이 발생할 수 있습니다. 반올림 오류로 인해 깊이 값의 작은 차이가 손실될 수 있기 때문입니다.

이러한 문제를 완화하기 위해 시간이 지남에 따라 다양한 기술이 개발되었습니다:

• 부동소수점 계산의 정밀도 향상
• 객체 위치 및 깊이 계산에 더욱 강력한 알고리즘 사용
• Z-fighting 감지 및 보정 메커니즘 구현

투명성 시나리오에서 Z-fighting 처리하기:

서로 겹치는 반투명 오브젝트를 처리할 때 몇 가지 기술을 사용하면 Z-파이팅 문제를 완화하거나 제거할 수 있습니다:

1. 알파 혼합: 투명한 개체를 결합하는 데 가장 일반적으로 사용되는 기법입니다. 알파 값(0~255)은 개체의 불투명도를 나타내며, 겹치는 두 개체의 알파 값이 다른 경우 가중 평균을 사용하여 결합된 색상과 투명도를 계산합니다.
2. 뎁스 필링: 이 방법에서는 각 반투명 레이어가 자체 깊이 버퍼를 사용하여 개별적으로 렌더링됩니다. 이 접근 방식은 레이어 간의 중첩을 최소화하여 Z-파이팅을 줄이는 데 도움이 될 수 있습니다.
3. 순서 독립 블렌딩: 일부 렌더링 엔진에서는 특정 개체 순서를 따르지 않고 투명 개체를 결합하는 순서 독립 블렌딩을 사용합니다. 이 기술을 사용하면 렌더링 순서에 관계없이 최종 결과가 일관되게 유지됩니다.
4. 화면 공간 정렬: 이 방법에서는 객체가 월드 공간 좌표(x, y, z)가 아닌 화면 공간 좌표(x, y)를 기준으로 정렬됩니다. 이 접근 방식은 2D 공간에서 오브젝트 간의 중첩을 최소화하여 Z 싸움을 줄이는 데 도움이 될 수 있습니다.

렌더링 엔진 및 라이브러리:

투명도와 겹치는 오브젝트를 잘 처리하는 인기 있는 렌더링 엔진과 라이브러리에는 다음과 같은 것들이 있습니다:

1. DirectX: Microsoft의 DirectX API는 알파 블렌딩 및 뎁스 필링에 대한 강력한 지원을 제공합니다.
2. OpenGL ES: OpenGL ES(Embedded Systems) 사양에는 투명 개체 시나리오에서 Z-fighting을 줄일 수 있는 순서 독립 혼합 같은 기능이 포함되어 있습니다.
3. Vulkan: Vulkan은 향상된 투명도 처리를 위한 다중 샘플 안티앨리어싱을 비롯한 고급 렌더링 기술을 지원하는 크로스 플랫폼 그래픽 API입니다.

---

“fixed-point or low-precision floating-point arithmetic for depth calculations.”
why cg use their?

CG (Computer Graphics) uses fixed-point or low-precision floating-point arithmetic for depth calculations because it provides a good balance between precision and performance.

Fixed-point arithmetic is fast, simple to implement, and requires minimal memory. However, it has limited range and accuracy compared to floating-point numbers. This can lead to issues with large scenes or complex geometry where the depth buffer overflows or underflows.

Low-precision floating-point arithmetic (e.g., 16-bit floats) offers better precision than fixed-point but is still more efficient than full IEEE754-compliant floating-point numbers (32-bit or 64-bit). It provides a good trade-off between accuracy and performance, making it suitable for many real-time graphics applications.

In CG, the depth buffer typically uses an unsigned integer value to represent the distance from the camera. This allows for fast and simple calculations using bitwise operations and shifts. However, this approach can lead to issues with large scenes or complex geometry where the depth values exceed the range of the unsigned integer type (e.g., 0-65535).

To mitigate these limitations, various techniques are used in CG:

1. Depth buffer scaling: Scaling the depth value before storing it in the buffer helps reduce overflows and underflows.
2. Clamping: Clamping the depth values to a specific range ensures that they remain within the valid range of the unsigned integer type.
3. Dithering: Dithering involves adding random noise to the depth values, which can help reduce artifacts caused by limited precision.

By using fixed-point or low-precision floating-point arithmetic for depth calculations and employing these techniques, CG applications can achieve a good balance between performance and accuracy in real-time graphics rendering.assistant

The use of fixed-point or low-precision floating-point arithmetic for depth calculations in Computer Graphics (CG) is due to the need for a trade-off between precision and performance.

Fixed-point arithmetic is fast, simple to implement, and requires minimal memory. However, it has limited range and accuracy compared to floating-point numbers. This can lead to issues with large scenes or complex geometry where the depth buffer overflows or underflows.

Low-precision floating-point arithmetic (e.g., 16-bit floats) offers better precision than fixed-point but is still more efficient than full IEEE754-compliant floating-point numbers (32-bit or 64-bit). It provides a good trade-off between accuracy and performance, making it suitable for many real-time graphics applications.

In CG, the depth buffer typically uses an unsigned integer type to store the depth values. This means that the precision of the depth values is limited by the number of bits used to represent them (e.g., 8-bit or 16-bit). To mitigate this limitation, various techniques are employed:

1. Clamping: Clamping ensures that the depth values remain within a specific range.
2. Dithering: Dithering involves adding random noise to the depth values, which can help reduce artifacts caused by limited precision.

By using fixed-point or low-precision floating-point arithmetic for depth calculations and employing these techniques, CG applications can achieve a good balance between performance and accuracy in real-time graphics rendering

---

To address these challenges, various techniques are employed:

1. Depth peeling: This method renders transparent objects multiple times with slightly offsetting Z-values to create the illusion of depth.
2. Order-independent transparency (OIT): OIT algorithms ensure that transparent objects blend correctly regardless of their order in which they’re rendered.

In addition to these techniques, there are other methods used for rendering transparent or translucent materials:

1. Screen-space ambient occlusion: This method uses screen space (the 2D image) to determine which pixels should be occluded by nearby objects.
2. Volumetric lighting: Volumetric lighting simulates the way light scatters through a medium, like water or fog, creating realistic effects for transparent materials.