게임 수학

그래프에서의 변화율을 판단하기

마법의 숫자 e e(2.718…)는 무리수로 어떠한 경우에도 기울기와 변화값이 동일하게 나타나는 수이다.

로그는 10^x^ = 3000 일때 logn10(10^x^) = logn10(3000) 으로 바꾸어 얼마만큼의 지수를 곱해야 해당값이 나오는지를 구하는 방법이다. 여기에 e를 넣게되면 반대로 자연로그를 써서 e의 승수를 구할 수 있다.

과학적 표기법

12.12 => 1.212 x 10^1^ => 1.212E1 0.053 => 5.3 x 10^-2^ => 5.3E-2

coordinate & intercept 기울기와 절편

기울기 계산식 = y2-y1 / x2-x1

연립 방정식 (치환, 소거)

f+t = 15 5f +3t - 10 = 45 그래프에 그려보자면… f = 5 ,.t = 10

평행선

연립방정식의 결과로 상수값이 다를경우

방정식 풀이법

• 1차 방정식의 표준형식 1차 연립방정식 (포물선) 접선 (1,0), (5,0) 이 주어질때 y = a(x-1)(x-5) y = ax^2^ - 6ax + 5a 해당 그래프의 꼭지점이 3,3을 지날 때 3 = 9a - 18a +5a a = -3/4

• 꼭지점 형식 y = ax^2^+bx + c y = a(x-p)(x-q) y = a(x-h)^2^+k (1,0)(5,0)(3,2) => 꼭지점이 3,2 즉 a(x-3)^2^+2에 대입가능함

1차 방정식 표준형식	꼭지점 형식	꼭지점 형식 변수
y = -2(x^2^ -10x + 16)	y = -2(x-5)^2^+3	y = a(x-h)^2^+k

각도와 원

부채꼴 : ark 둘레 : 2πr

각도와 라디안

각도 degree : 원을 360도 기준으로 나눈것 radian : 원의 둘레 기준으로 2πr 개의 ark로 구성된 원의 반지름에 대한 호의 길이이다.

즉 라디안은 l / r 으로 호에 대한 반지름의 비율이다.

rad * Mathf.Rad2Deg( 180/ π) => degree 각도가 된다. degree * Mathf.Deg2Rad( π / 180) => radian이 된다.

• 1. 120 도 => radian
     • 120 x (π /180) => 2/3 π
• 1. π / 4 => degree
     • π / 4 x (180 / π ) => 45 도 radian to degree에서 전체 radian이 2π 란것을 감안하면 2π = π /4 x a 여기서 a가 8일때 전체 라디안값이 나오므로 360 / 8 => 45도로 구할수도 있다.

피타고라스의 정리

c^2^ = (a+b)^2^ - 2ab c^2^ = a^2^+2ab+b^2^ -2ab c^2^ = a^2^+b^2^

대각선 이동에 사용하는 피타고라스..

sin cos tan

원 내부에 삼각형을 그릴때, 밑변은 cos 높이는 sin이 된다. 이 둘은 삼각형의 특성상 서로 반비례하는 값을 지닌다. 따라서 sin cos tan의 성질은 삼각형의 성질을 따른다.

• sin : 길이
• cos : 밑변
• tan : 반지름에 수직인 선 sin / cos 예각의 높이변과 밑벼의 비를 탄젠트라 한다.

각이 90도일때 각 sin cos tan는…

• sin (90) = 1 (90도 , 270도 일때 삼각형의 높이값이 최대)
• cos (90) = 0 (0도, 360도 일때 삼각형 밑변 길이 최대)
• tan (90) = N/A (0 으로 나눈 값이므로 측정 불가)

---

30도의 경우

• sin (30) = 1/2
• cos (30) = √3 /2
• tan (30) = √3/3

60도의 경우

• sin (60) = √3/2
• cos (60) = 1/2
• tan (60) = √3

서로 역수에 있다는 사실을 알 수 있다. 위의 두 각 모두 직각 삼각형의 1 : √3 / 2 비율에 의해 구할 수 있었다. math 와 같은 라이브러리 사용시 인자는 모두 라디안 값으로 판단한다.

사분면 각도 기준 sin cos tan의 값이 양수 음수가 된다.

삼각형 빗변 대변 인접변 공식 (SOH, CAH, TOA)

세타를 기준으로 인접변, 대변, 빗변 (빗변은 항상 직각에 맞은편으로 동일) 을 정할 수 있다.

역함수

역함수는 sin cos tan 함수의 역수이며 arc를 붙인다 이는 해당하는 삼각함수 각도를 구할때 사용할 수 있는데 sin(Θ) = 3/ 5 Θ= asin(3/5) => 36.89의 값으로 theta를 구할 수 있다.

빗변 => 15^2^ = 12^2^ + 9^2^ sin(Θ) = 9/15 => 0.6 Θ = arcsin(0.6) => 36.86…. Θ 의 값을 구하기 위해 역삼각함수를 취해준다.

sin(Θ) = 12/c sin(52) * c = 12 0.78 * c =12 c = 15.3….

직각 삼각형이 아닌 경우의 각도 법칙

사인 법칙

사인 각도 법칙

a/sin(A) = b/sin(B) = c/sin(C)

6.9/sin(32) = 5/sin(B) =>sin(B) = 5sin(32)/6.9 B = sin^-1^( 5sin(32)/6.9 ) B = 22.58

단 이를 활용할 때는 각의 값이 두 개 존재할 수 있으므로 조심하여야 한다. 4분면에서 sin값이 양수가 되는 지점은 1,2사분면인데, 이때 2개의 값이 답이 될 수 있다. 그렇기에 다른 각도의 정보가 더 필요하다

코사인 법칙

코사인 각도 계산 법칙

c^2^ = a^2^+b^2^ - 2ab cos(c)

36= 16 + 25 - 40 cos(b) -5 = -40 cos(b) 1 = 8cos(b) cos(b) = 1/8 b = cos^-1^(1/8)

사인파 조작

a sin(bx -c) +d a : 진폭 (파형의 높낮이) b : 파형의 빈도 c : 파형을 c만큼 진행시킴 d : 파형을 d만큼 y축으로 높임

파장의 합성

1. 파형의 보강 간섭
2. 파형의 상쇄 간섭
3. 파장의 총 크기 -> magnitude

벡터와 행렬

벡터 표기법 : 위에 방향을 표시

단위 벡터 ^ (유닛 벡터) : 길이가 1인 벡터 (햇 벡터) 위치 벡터: OA, OB 변위 벡터: AB (3,1) 벡터간의 차이 벡터 넓이 : ||OA||

벡트 크기와 크기의 제곱

이전 피타고라스 정리에서 처럼 벡터의 선을 아래로 이으면 직각삼각형을 만들 수 있다.

서로 다른점을 기준으로 하는 벡터의 넓이를 구하려면 이전 삼각형의 기울기 값을 구하던 방식을 쓰면 된다. ||V|| = √ (x2 - x1)^2^ + (y2-y1)^2^ ||OA|| = √3^2^ + 4^2^ => 5

이는 3차원을 사용할때도 동일하게 적용된다. 다만 이 연산을 자주 수행하게 될 경우 시간이 오래걸린다. 그렇기에 크기의 제곱을 사용할 필요가 있다.

크기의 제곱은 루트 연산을 줄여줌으로 매우 많이 사용되나, 벡터의 값을 UI에 표시하는등 실제값이 필요할때 제곱근으로 변환한다.

위치 벡터에 사용 vector.Magnitude (v) vector.sqrmagnitude(v)

변위벡터에 사용 vector.distance(a,b) vector.sqrdistance(a,b)

좌표계

게임엔진에는 z축이 화면 안으로 들어가는 왼손 좌표계 마야 맥스 블렌더와 같은 3D 모델링 프로그램은 오른손 좌표계를 사용한다.

유니티에 블렌더 오브젝트를 임포트할때 축이 바뀌는 경험이 있었는데, 해당 이유 때문이었음. 결과적으로 y축과 z축의 읽어들이는 순서를 바꾸면 된다.

이해가 안 간다면 오른손 좌표계에서 y축과 z축을 바꾼 뒤 x축으로 90도 돌려보자

왜 엔진은 오른손 좌표계를 사용하지?

백터의 덧셈

백터의 덧셈은 정수 좌표계의 덧셈과 동일하게 수행되며 교환법칙이 성립된다. 마찬가지로 벡터는 방향을 가지기에 벡터의 차이는 a + (-b) 벡터의 합이 된다.

스칼라 곱셈

velocity = vector (방향과 크기) speed = scalar (크기)

스칼라 x 벡터는 단순히 스칼라 값을 벡터에 곱해주면 된다.

벡터의 정규화

벡터를 다루기 쉽도록 단위벡터로 만들어주는 과정을 벡터 정규화 vector Normalize라고 한다.

단위벡터를 만드는 방법은 벡터 / 벡터의 넓이 를 구해주면 된다.

	V		= √ (x2 - x1)^2^ + (y2-y1)^2^
단위 V = V /		V		이다.

예를 들어 1,1 벡터의 경우 이 둘의 넓이를 구하면 √2 인데, 이 넓이값을 각 x, y에 해당하는 값에 나눠주면 된다. (1/√2, 1/√2)

유니티에서 vector.forword, vector.right를 사용하여 캐릭터를 움직였을때, 캐릭터가 대각선으로 더 빨리 가는 경험을 한 적이 있다면 이 단위벡터를 구하는 과정을 거쳐주지 않아서 그런다.

0 벡터

크기가 없으며 방향 정보가 없는 벡터를 0벡터라고 한다. 0벡터는 벡터의 초기 상태로 나타내기도 하며 0,0 x (x,y) => (0,0)이 된다. 이는 스칼라의 0과는 엄연히 다르다. 벡터의 0은 스칼라 0과 다르게 시간을 기점으로 벡터의 0,0 을 표기할 수 있기 때문이다.

내적

벡터의 내적은 두 벡터간의 cos인 각을 쟤기 위해 사용한다. 이는 내적이 두 백터간의 방향 유사성을 나타낸다고 볼 수 있다.

단위 벡터 만들기

1. aㆍb = (ax * bx) + (ay * by) + (az * bz) « 내적 공식

2. v^ = v /

   V

3. aㆍb =

   a

   b

   cosΘ , aㆍb^(단위) =

   a

   cosΘ (cos 삼각함수 공식과 유사함)

4. 이를 각도 계산식으로 바꾸게 되면, Θ = acos (aㆍb/

   a

   b

   ) 여기서 단위벡터일 경우 Θ = acos (aㆍb)

ex) 만약 1,0 적이, -3,4 위치에 플레이어가 있을 때 적이 방향 벡터 기준으로 90도 탐색한다면 탐색될것인가?

dot 연산으로 구하기

• aㆍb =

  a

  b

  cosΘ (a, b != ^(단위일 경우 크기는 1))

• cosΘ = aㆍb /

  a

  b

• Θ = acos ( aㆍb /

  a

  b

  )

• Θ = acos ( (1 * -3) + (0 * 4) / 5 ) a는 (단위벡터로 사라짐)
• Θ = acos(-3/5) => 126º

사인 법칙

a/sin(A) = b/sin(B) = c/sin(C)

코사인 법칙

c^2^ = a^2^+b^2^ - 2ab cos(c)

외적

두 벡터에 수직인 벡터를 만들고 그 벡터의 넓이를 정의하는 것.

a = (0,0,1) , b = (1,0,0)

외적 가위곱의 동일성 => A x B = -B x A ( 이 이유는 벡터의 외적이 C 벡터를 구하는 것이며, 넓이는 위 아래 방향으로 나올 수 있기 때문이다. 마찬가지로 각도가 0 또는 π일 경우 넓이가 없으므로 값이 0이다)

이로써 외적은 벡터간의 교환, 결합 법칙이 성립하지 않는다.

벡터 외적의 결과값은 두 벡터의 수직인 선이며, 크기는 두 벡터의 넓이 값이다.

[내적 외적] (https://wikidocs.net/22384)

---

---

외적의 y 성분을 구하는 과정을 행렬식을 통해 설명하겠습니다. 외적은 두 벡터의 3x3 행렬식으로 표현할 수 있습니다. 벡터 A와 B의 외적을 구할 때, 행렬식은 다음과 같이 구성됩니다:

벡터 A = {A.x, A.y, A.z} 벡터 B = {B.x, B.y, B.z}

외적 C = A × B는 다음과 같은 행렬식으로 표현됩니다:

i j k

A.x A.y A.z

B.x B.y B.z

여기서 i, j, k는 단위 벡터입니다. 이 행렬식을 전개하면 다음과 같은 결과를 얻습니다:

C = i * (A.y * B.z - A.z * B.y) - j * (A.x * B.z - A.z * B.x) + k * (A.x * B.y - A.y * B.x)

따라서, 각 성분은 다음과 같이 계산됩니다:

• C.x = (A.y * B.z) - (A.z * B.y)
• C.y = (A.z * B.x) - (A.x * B.z)
• C.z = (A.x * B.y) - (A.y * B.x)

---

---

반사

unity reflection

반사의 식 r = 2(-a dot n) x n + a

2(-((1/3 * 2/7) + (-2/3 * 6/7) + (-2/3 * 3/7))) 2(-((2/21) + (-12/21) + (-6/21))) 2(16/21) * (2/7, 6/7, 3/7) + (1/3, -2/3, -2/3) => (0.4,1.3,0.6) + (0.3, -0.6, -0.6) r = (0.7,0.,0)

평면으로의 사영

벽 방향으로 계속 가다보면 언젠가 벽의 옆면으로 이동하는걸 볼 수 있는데, 이것은 사영되기 떄문이다. 그림의 예시를 보면, n^ 방향이 x만큼 인 normal vector가 있는데, 이에 사영하게 되면 결과적으로 x만 삭제된다. 그럼 y와 z만 남게되는데 이 방향으로 사영하게 되는것이다.

아래 공식을 보자

p = a - (n^ x aㆍn^ / n^ㆍn^)   

난데없이 자기 자신을 내적하는데, 이는 당연하게도 단위 벡터라면 자기 자신을 기준으로 평행하기에 1의 값이 나온다. 여기선 이 값을 넓이로 사용하기 위해 내적 연산을 한다고 함.

벡터수식 모음

// 두 벡터간 각도 구하기
내적 = ||A||||B|| SIN()

// 내적의 공식
aㆍb  = (ax * bx) + (ay * by) + (az * bz)


// 두 벡터의 수직인 벡터 생성하기
외적 = ||A||||B|| COS()

// 외적의 공식
C.x = (A.y * B.z) - (A.z * B.y)
C.y = (A.z * B.x) - (A.x * B.z)
C.z = (A.x * B.y) - (A.y * B.x)


// 벡터의 넓이
||V|| = √ (x2 - x1)^2^ + (y2-y1)^2^

// 단위 벡터
v^ = v / ||V||

(https://community.gamedev.tv/t/reflection-geometric-interpretation/158550)
// 반사 (cos, sin과의 연관관계?)
r = 2(-aㆍn) x n + a

// 평면에 사영
p = a - (n^ x(곱셈) aㆍn^ / n^ㆍn^)

행렬이란?

벡터들의 묶음.

행 백터 : 행 기준으로 정렬된 벡터 열 백터 : 열 기준으로 정렬된 벡터

게임엔진에서는 이 행렬중 TRS를 많이 사용하는데, 이동 회전 크기에 대한 행렬이다.

전치 행렬의 행과 열을 바꿔주는 것이다. 이 행렬이 전치된 여부는 T 표시로 확인할 수 있따.

행렬의 합 및 스칼라 곱셈

행렬의 합은 매우 간단하나, 조건을 지켜줘야 한다.

1. 계산하려는 행렬의 크기가 동일리해야 한다

스칼라 곱셈

A = [4 5] [3 2] 2A = [4x2 5x2] [3x2 2x2]

나누기의 경우도 똑같이 수행해주면 된다.

인접행렬

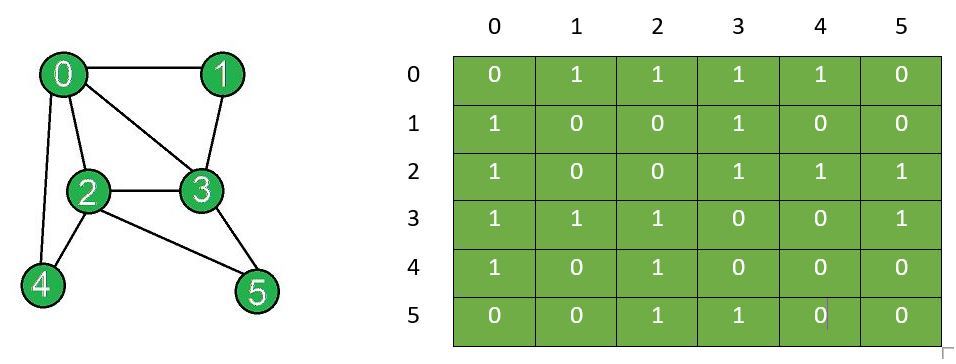
인접행렬의 경우 방향성이 없을때 대칭을 이룬다.

행렬의 곱셈

행렬에 n 제곱을 할 경우, n번만큼 움직여서 이동할 수 있는 경로의 수를 보여준다.


행렬의 곱셈 순서. A의 행과 B의 열 순서대로 내적이 진행된다. 이로써 내적은 3 X 4로 총 12번 일어나게 된다.

행렬간의 곱셈은 A B 기준으로 A행 과 B 열간의 내적을 해주면 된다. 총 16번의 내적을 사용하게 되며, 결과는 표와 같이 나온다.

행렬간의 곱셈을 할 때 중요한것은 곱해지는 행렬 A의 열과 B의 행이 결과 행렬로 나온다는 것이다. 그러므로 행렬간의 교환법칙은 성립하지 않는다.

단위 행렬

단위행렬의 특징으로는 대각선의 부분은 모두 1로 채워지게 된다는 것이다. 이러한 성질에 의해 AxB != BxA 였던것과 반대로 순서가 바뀌어도 성립하게 된다.

A = [ 1 2] [ 3 4 ] B = [ 1 0 ] [ 0 1 ] 이라고 할 때, 해당 결과값은 온전히 A와 동일하게 나오게 된다. 그렇다면 단위 행렬은 왜 사용하는걸까?

행렬식

행렬식이란, 역행렬이 존재하는지를 확인하기 위한 스칼라 값이다. A x B = C라는 행렬식이 존재할 때 역으로 내적을 되돌리는 것 보다 B = A^-1^ x C 를 수행하면 쉽게 B의 값을 찾을 수 있다. 수학에서 역수를 취하여 찾듯이, 행렬에서는 역행렬을 구하여 찾는것이다.

이 역행렬을 구하는것이 행렬식이다.

행렬식은 위의 순서대로 0,0에 해당하는 수부터 열 행에 해당하는 요소를 제외하고 가위곱을 실시한다. 이를 A0에 해당하는 행들에 대해 수행하며 최종 결과물을 반환한다. 이를 라플라스 전개라 한다.

- + - + // 각 숫자 사이에 적용된다.
(-3) -(-12) + (-9) => 0
0 이므로 비가역행렬이다 (역행렬이 존재하지 않는다)

역행렬

A = [5 4 ] [2 1 ]

(5 x 1) - (4 x 2) = - 3 detA = -3

역행렬을 만들기 위해서는 위에서 구한 행렬식 결과값과 기존 행렬을 변형시킨 값이 필요하다

간단한 역행렬 계산
[5 4 ]   =>  [ 1 -4 ]
[2 1 ]		 [-2 5 ]

첫 가위곱 대상은 위치를 바꿔주고
두번째 가위곱 대상은 부호를 바꾸어준다.

A^-1^ = detA x
[ 1 -4 ] [-2 5 ]

A^-1^ = 1/-3
[ 1 -4 ] [-2 5 ]

A^-1^ = [ -1/3 4/3 ] [ 2/3 -5/3 ]

3차원 행렬도 동일하게 진행된다.

1. 행렬의 행렬식을 통해 역행렬이 존재하는지 파악. (행렬식 사용)
2. 2x2 행렬로 바꾸로 해당하는 행렬들을 나누고 각 행렬식 계산 (소행렬식 구하기)
3. 부호를 바꾸어 여인수 행렬을 구함 (여인수 행렬 구하기)
4. 여인수 행렬을 전치시킨 후 행렬식 스칼라 값을 행렬에 곱해준다. (수반행렬 구하기)

회전과 보간

벡터의 방향

3차원에서의 방향의 각도를 알고 싶다면 어떻게 해야할까?

x = 3, y= 5, z= 4 일 때, atan를 사용하여 각도를 모두 구한다. 하지만 해당 방법은 꽤나 손이 많이 가는데.

||V|| = √ a^2^ + b^2^ + c^2^ 를 하게되면 빗변에 해당하는 벡터를 얻을 수 있다. ||V|| = √ (x2 - x1)^2^ + (y2-y1)^2^ 벡터의 넓이를 가져와 인접변과 빗변을 사용하는 cos 를 세 각도에 모두 적용해주면 위의 결과를 확인할 수 있다.

처음 계산보다는 매우 간단하게 계산할 수 있음.

허수

![Lateral Numbers – How ‘Imaginary Numbers’ May Be Understood

Heurist.me (Carey G. Butler)](https://heurist.me/wp-content/uploads/2017/11/rbi0y.png?w=584)

허수는 곁수라고도 부르는데, 실수의 곁에 자리하고 있어 곁수라고도 부른다. 허수는 i라고 부르며 이 i는 제곱하면 -1이 되는 수이다. 즉 √-1 = i

허수는 제곱을 진행함에 따라 i, -1, -i, 1, i로 반복되는데, 이는 좌표상으로 회전하는것과 같다. 오른쪽 위를 보면, y= x^2^ -1일때 -1, 1의 근을 가지는데 반해 y= x^2^ +1 일때는 허수의 근이 존재하게 된다.

허수좌표의 근들을 표시한 이미지로, 실제 좌표평면의 포물선에 해당하는 근들을 허수부로 나타낸 결과이다.

복소수

2차원 좌표계를 사용하였듯이, 복소수의 좌표계 또한 벡터의 스칼라 덧셈과 다르지 않다. 우리가 복소수를 사용하는 근본적인 이유는 실수부를 복소수 평면으로, 이 복소수 평면을 사원수로 만들기 위함이다.

복소평면

앞서 우리가 복소수 평면을 사용하는것은 사원수를 만들기 위함이라 하였는데, 복소수는 각도의 변화를 나타내기 매우 좋기 때문이다. 복소수간의 곱셈은 실수와 동일하게 진행되며, 계산 결과 i^2^를 -1로 표기할 수 있어 간단히 떨어진다.

이를 이용해 (2+2i), (3+1i) 둘을 atan로 각도를 구하면 atan(2/2) , atan(1/3)이 되므로 각각 45, 18.4도가 나온다. 신기하게도 이 둘의 각도를 더하면 위에서 구한 4+8i에 해당하는 각도 63.4도가 나오게 된다. 결과적으로 두 복소수를 곱하면 복소평면에서 회전을 하게 된다.

이러한 형식을 직교 형식이라 한다.

(a+bi)(c+di) 복소수간 곱셈은
(ac - bd) + (ad + bc) i 로 나타낼 수 있다.

// 복소수간 좌표 각도 계산은 atan 시켜주면 된다.

(2+2i)(1+i) = 4i => 90도의 각도를 가지며 (2+2i)^2^ = 8i => 이 또한 90도의 각도를 가지게 되나 (atan(8 / 0)) 두 배의 크기를 가진다.

결과적으로, 복소평면에서 복소수간의 곱셈은, 해당하는 만큼 각도를 회전시킨 것과 동일한 결과를 얻을 수 있다.

극좌표

a = r < θ 이러한 형식으로 표시하는것을 극좌표라고 한다. 이러한 극좌표는 삼각함수로 표현될 수 있다.

3+ 2i = √13 < 33.7º
a = r < θ

//(r은 크기로 두 각에 해당하는 라디안에 r만큼 곱해준다.)
a = r(cos θ + i sinθ)
a = √13 (cos (33.7) + i sin(33.7))
a = 3 + 2i

두 각도의 극좌표 계산식

// 두 각도의 합
axb = rs(cos(θ + Φ) + i sin(θ + Φ))
// 두 각도의 차
a/b = r/s(cos(θ - Φ) + i sin(θ - Φ))

두 표기방법을 모두 사용하면 쉽게 풀 수 있을것이다.

회전 행렬

물체를 회전시키기 위해서는 회전 행렬이 필요하다.

이 회전 행렬은 단위벡터와 같이 변하지 않는데, 해당 열 벡터에 맞춰 행렬식에 값을 넣어주면 된다.

위 그림처럼 각도를 30만큼 옮겨줄 경우, 기준점 0,0 벡터를 기준으로 모든 점들이 각도만큼 회전하게 된다. 나머지 점들 모두 계산을 하게 되면

a = (0,0) 기준 좌표 b = (1.73,1) c = (0.72, 2.72) d = (-1, 1.72)

오일러 행렬

3차원의 회전 또한 2차원처럼 회전축을 제외한 나머지 행렬의 내적을 시켜주면 된다.

회전을 시킬 때는 단위 행렬을 참고하여 회전하려는 기준축으로 움직여주면 된다. 이동한 축에 대한 (y가 z축 기준으로 회전 할 때, -sinθ 만큼 이동) 변화로 행렬이 이루어진다.

• 항상 회전은 시계 방향으로 이루어진다는것을 기억하자.
• 오일러 회전을 사용할 때는 z-x-y , 피치-롤-요 순서대로 움직인다.
• 회전 하는 순서에 따라 회전 방향이 바뀌므로 이를 유의해야 한다 (종속성)

짐벌락

오일러각 회전을 사용하게되면 짐벌락이라는게 생겨버린다.

짐벌락이란? 오일러 각을 이루는 각 축들이 겹치게 되었을 때, 축에 대한 자유도를 상실하게 된다.이는 각 축들이 하이라키상태로 존재하기 때문에 하위 축들이 영향을 받기에 생기는 문제점이다.

오일러 회전이 정해지는 순서는, 해당 물체가 가장 많이 수행되는 축을 기준으로 하이라키기준을 메긴다. 그럼으로 하이라키를 고려하여 움직이면 짐벌락을 최대한 피할 수 있다.

사원수란 무엇인가?

2차원 또는 3차원에서의 각도 계산에서 오일러각을 사용하였는데, 이때 실수, 허수부로 이루어진 복소평면을 사용했다. 반대로 사원수는 하나의 실수부와 3개의 허수부로 구성된 좌표계로 짐벌락을 피할수 있으며, 회전의 취소 또한 자유롭다.

위는 쿼터니언의 좌표계를 나타낸것인데, 두개의 허수부의 인자들이 0인 경우 복소평면이 되며, 3개가 허수부인 경우 실수가 된다. 이를 통해 4차원의 좌표 계산을 수행할 수 있게 되는것이다.

사원수 곱셈 -1-

사원수를 서로 곱하게 되면 어떻게 될까? 우선 간단히 나타내기 위해 허수부 테이블믈 만들어준다.

자신과 곱할경우, 익숙한 모양처럼 (단위행렬) -1 이 된다. 행렬 연산에서 처럼 사원수의 곱셈은 교환법칙이 성립하지 않는다.

한가지 주의해야 할 점은 i, j, k는 모두 허수부이며 i^2^ = j^2^ = k^2^ 라는 점이다. 즉 ijk = -1 이다.

위의 결과는 두 사원수를 곱한 것으로 모두 분배법칙을 사용해주면 위의 복잡한 식이 나오게 되는데, 이중 i^2^과 같이 = -1로 나타낼 수 있는 것들을 단순화 해준다.

이후 허수부에 해당 하는 요소끼리 묶으면 위처럼 정렬된 식을 구할 수 있다.

언뜻 보기에 실수부와 허수부가 나뉘기에 사원소처럼 보이기도 하며, 4차원 벡터의 값이 된다.

사원수 곱셈 -2-

내적과 외적은 이 사원수 곱셈을 처리하기 위해 고안된 것이다.

사원수 곱셈 1에 이어서 2로 넘어가보자. 여기선 사원수를 간단한 수식으로 바꾸는 과정을 다루는데, 실수부 w와 나머지 허수부의 형식으로 묶어 표현하면 아래와 같이 표현된다.

이는 사원수간의 곱 결과를 행렬로 저장한것이며, 서로간에 곱하는 벡터 요소를 바꾸어도 결과는 동일하게 나온다.

사원수 회전 -1-

사원수 기준으로 하나의 축을 지정할 때, 나머지 두 허수부를 곱하면 축 기준 방향으로 회전하게 된다.

4차원의 축을 기준으로 자신을 제곱하게 되면 실수부로 나타내지는데, 3차원 상의 좌표축에선 표시되지 않는다 (허수부 3차원 좌표이기에).

아래 그림을 보면 복소평면 기준으로 허수부에 곱하게 될 수록 원형으로 회전하게 된다. (허수부간의 곱을 통해 나온 실수는 아래 복소평면 좌표예서의 변화를 확인 할 수 있다.)

위에서 예시를 들었던 4차원에서의 축 변환 결과를 우리가 확인할 수 없는 이유가 바로 이 예시이다.

사원수 켤레 (conjugate)

기존 사원수의 벡터 (허수부)를 음수로 나타낸것이다.

사원수 회전 -2-

사원수 회전식은 v` = q v q 이다.

복소평면을 기준으로 바라볼 때, v` = cosθ + isinθ

이를 사원수 기준으로 변환하면 허수부를 벡터로 묶을수 있다. 이 벡터가 쿼터니언 회전축이 된다.

q = cosθ /2 + vsinθ /2
== q = cosθ + xsinθi + ysinθj + zsinθk

다만 쿼터니언 곱의 최대 단점은 회전각도가 180도로 제한된다는 것이다.

그 이유는 쿼터니언 곱을 수행할 때, 서로 반대 방향으로 축은 상쇄되지만 회전 각도는 두 배로 증가하기 때문이다 (복소평면을 기준으로 보자면)

//실수, 허수부를 반으로 나눈다.
cosθ /2 + vsinθ /2

선형 보간

점 사이의 값이 실제 무엇일지 예측하는 방법이다.

• 선형 보간의 식 = a + (b-a ) x t (t에 따른 b 만큼의 변화율)
• 선형이 아닌 사인, 2차함수로 사용하여 보간을 할 수도 있는데, 이는 Easing 함수의 범주로 묶인다.

구면 선형보간 (SLERP)

구면 선형보간이란, 둘 사이의 점을 직선 대신 호의 모양으로 보간하는 방법이다.

구면선형보간의 경우 내부 삼각함수의 공식에 따라 계산되며 t의 영향을 받아 한쪽 항이 생략될 수도 있다. 이는 각 점에 따른 변화율의 값을 더해 얼마나 보간되었는지 판단할 수 있다.

실질적으로 구면선형보간을 수행할 때, 쿼터니언은 해당하는 각도의 벡터값을 구하고 해당하는 호에 맞춰 정규화를 수행해준다.

이징 함수

다양한 이징 함수

---

---

통계와 데이터

데이터를 표현할 때는 데이터의 성격을 파악하고 여기서 얻어야 할 정보를 도출해야한다.

시그마 표기법

시그마는 sum을 표기하는 방법으로 lower bound, upper bound가 정해지면 오른쪽의 expression 기준으로 합을 진행한다.

이처럼 시그마를 통해 합을 계산하는 식을 직관적으로 세울 수 있다. goals 처럼 정해야 하는 기준이 확실한 경우 범위를 따로 지정하지 않아도 된다.

평균

• 평균 : n개의 요소들의 평균값, 왜곡 발생가능
• 최빈값 : 가장 많이 나타난 값
• 중앙값 : 데이터의 가운데 값

극단치

평균을 벗어나 극단적으로 치우친 값을 처리.

• 무시
• 제거
• 조정

왜도 (skew)

비대칭도로써 확률 분포의 비대칭성을 나타낸다.

---

사분위간 범위

사분위의 범위를 통해 유의미한 통계를 낼 수 있다.

사분위는 중앙값의 중앙값을 반복하여 진행하며, Q1 - Q3은 사분위의 범위가 된다.

표준편차

• 분산 : 𝛔^2^이며 평균을 기준으로 얼만큼 떨어져있는지 나타낸다, (수치 - 산술평균)^2^ / n 으로 구할 수있다.
• 표준편차 : √ 𝛔^2^ 이 값은 평균으로 만큼 값들이 얼만큼 차이나는지를 표준화 시킨것이다. 이것을 기준으로 (산술평균 - 표준편차)를 수행하면 내부에 속하는 표준값과 극단치를 쉽게 확인할 수 있다.

s는 데이터 셋의 일부를 가져와 표본집단으로 삼아 표준편차를 낸 결과이다. 공식에서 N 이 N-1로 바뀌었는데, 이는 더 작은수로 나누어준 표준편차의 값이 살짝 커졌기에 표본을 위한 여유분의 값을 준 것이다.

상관 (Correlation)

완벽한 양의 상관관계

완벽한 음의 상관관계

인자들이 서로간의 얼마만큼의 상관관계를 지녔는지 파악할 수 있다. 일반적으로 0.7~0.9는 강한 상관관계를 가졌다 볼 수 있다.

인과(Causation)

데이터의 분석과 해석은 별개의 일이다.

데이터 정규화

데이터의 규모가 다를때, 이를 데이터 정규화를 통해 쉽게 분석할 수 있다.

(b-a)f(x) + a 로 데이터의 범위를 재정의 해주면 범위의 크기를 바꿀 수 있다.

확률의 기초

상호배반적인 경우 위의 공식을 따르게 된다.

연속 시행

연속 시행의 결과를 얻기 위해선 확률을 곱해주어야 한다.

독립 사건과 종속 사건

• 독립 시행의 연속: 1/6 * 1/6 주사위

• 이전 확률이 영향을 줄 경우 : 최소 1개의 에이스 뽑기

  • (4/52 * 3/51) + (4/52 * 47/51) + (48/52 * 4/51) = 14.93%

여사건 법칙

어떤 사건이 일어날 확률을 P(A)라 할때, 이의 반대되는 확률은 1-P(A`)이다.

여사건을 이용해 한번도 등장하지 않는 경우를 판단하게 될 경우 쉽게 문제를 풀 수 있을지도

이론적 확률과 경험적 확률

큰수의 법칙: 일정 이상의 모수가 모일 경우 이론적 확률에 근접한다.

평균값 정리

흔히 도박사의 오류라 칭한다. 상관관계가 없는 확률 사이에 패턴을 찾아내려고 하는 실수를 뜻하며, 플레이어의 부정적 감성을 제거하기위해 인위적으로 확률에 어드밴티지를 추가할 수도 있을것이다.

베이즈의 정리

베이즈 정리를 사용하면 해당 식으로 확률을 계산할 수 있다.

경품이 있는 문을 선택할 때, 진행자가 플레이어의 선택, 경품이 있는곳을 제외한곳의 문을 열어주는 경우를 판단해보면, 베이즈 정리를 이용해 확률을 계산할 수 있다.

결과적으로 추가적인 정보를 얻게 되어 확률이 높아지게 된다.

2차 세계대전 당시 앨런 튜닝이 베이즈 정리를 통해 에니그마 암호를 해독했다.

누적분포함수

값의 누적치를 계산하여 나타낸 분포 함수이다. 자세히 보면 개별 1~5 확률과 9~13 확률이 동일하다.

엘로 평점 시스템

위는 플레이어간의 승점차이 기준으로 이길 확률을 계산한것이다. 아래는 승패 결과에 따라 얻게 될 득점을 계산한것으로, 두 식 모두 상수를 사용함으로 이를 잘 조정해주어야 한다.

A, B 플레이어의 승률과 승패에 따른 점수 변화