[자료구조/ 알고리즘] BackTracking

BackTracking

최적의 경로 찾기를 위한 길찾기 알고리즘.

Problem Types

1. Decision Problem - check for feasible(yes or not) solution

   구현 가능한 지에 대한 문제

2. Optimisation Problem - find best solution

   최적의 문제 결과 도출 (minimum resource)

3. Enumeration Problem - find all solution

   도출 가능한 모든 경우의 수 판단

BackTracking은 기본적으로 recursion 개념을 수행한다.

BackTracking과 Recursion의 차이점

가장 큰 차이점은 아래와 같다

Recursion	BackTracking
재귀 함수는 자신의 복사본을 호출하고 원래 문제의 더 작은 하위 문제를 해결하는 방식으로 특정 문제를 해결합니다.	모든 단계에서 역추적을 통해 해결책을 제시할 수 없는 선택지를 제거하고 해결책을 제시할 가능성이 있는 선택지로 진행합니다.

---

BackTracking on Array

#include<iostream>
using namespace std;

void PrintArray(int *arr, int e)
{
    for (int t = 0; t < e; t++)
    {
        cout << arr[t] << ", ";
    }
}
// int *arr just gets first element's of pointer in arr[]
void fillArray(int *arr,int s,int e, int val)
{
    # base case
    if(s == e)
    {
        //can't use foreach cause we can't specify array size with pointer
        // print out array
        for (int j = 0; j < e; j++)
        {
            cout << arr[j] << ", ";
        }
        return;
    }
    # rec case
    arr[s] = val;
    fillArray(arr,s+1,e, val+1);

	# backtracking step
    arr[s] = -1 * arr[s];
    cout << endl;
    PrintArray(arr,e);
}

int main()
{
    int arr[100] = {0};
    int e;
    int val;
    cin >> e >> val;
    fillArray(arr,0,e,val);
    return 0;
}
Result : n = 3, val = 1
1, 2, 3,
1, 2, -3,
1, -2, -3,
-1, -2, -3,

결과를 보면 call stack에 적재된 순서에 따라 재귀 함수를 호출하고 BackTracking 부분이 실행되는 모습을 볼 수 있다.

    # backtracking step
    arr[s] = -1 * arr[s];
    cout << endl;
    PrintArray(arr,e);

위에서 작성한 부분이 backTracking 구현부가 된다.

BackTracking on Vectors

#include<iostream>
#include<vector>
using namespace std;

void pirntArray(vector<int> &arr)
{
    for (auto &&i : arr)
    {
        cout << i <<", ";
    }
}

// reference shared accross all func called
void fillArray(vector<int> &arr,int i,int e, int val)
{
    //base case
    if(i == e)
    {
        pirntArray(arr);
        return;
    }
    //recursion case
    arr[i] = val;
    fillArray(arr,i+1, e, val+1);
    // backtracking step
    if((arr[i]-1)&(arr[i]) != 0)
        arr[i] = 0;
}

int main()
{
    int n;
    int val;
    cin >> n >> val;

    vector<int> arr(n);
    fillArray(arr,0,arr.size(),val);
    cout << endl;
    pirntArray(arr);
}

Result: n :10, val :3
3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
3, 0, 5, 0, 7, 0, 9, 0, 11, 0,

기본적으로 C++의 STL은 passed by value다. 만약 이를 고려하지않고 위의 코드를 수행한다면 재귀호출이 일어나고 종료되는 시점에서 element를 가진 vector는 삭제되고 이전에 적재된 vector가 call stack에 존재하게 된다.

// 레퍼런스 타입으로 가져오지 않을 경우
n :5, val : 1
1, 2, 3, 4, 5,
0, 0, 0, 0, 0,

그러니 Vector Container를 사용할 때 call stack의 현재 위치에 따라 vector의 요소가 변하는 것이다. 이를 방지하기위해선 레퍼런스 타입으로 매개변수를 가져오는것을 잊지말자.

Find Subsets (Ordering)

모든 부분 문자열을 출력하는 코드이다. 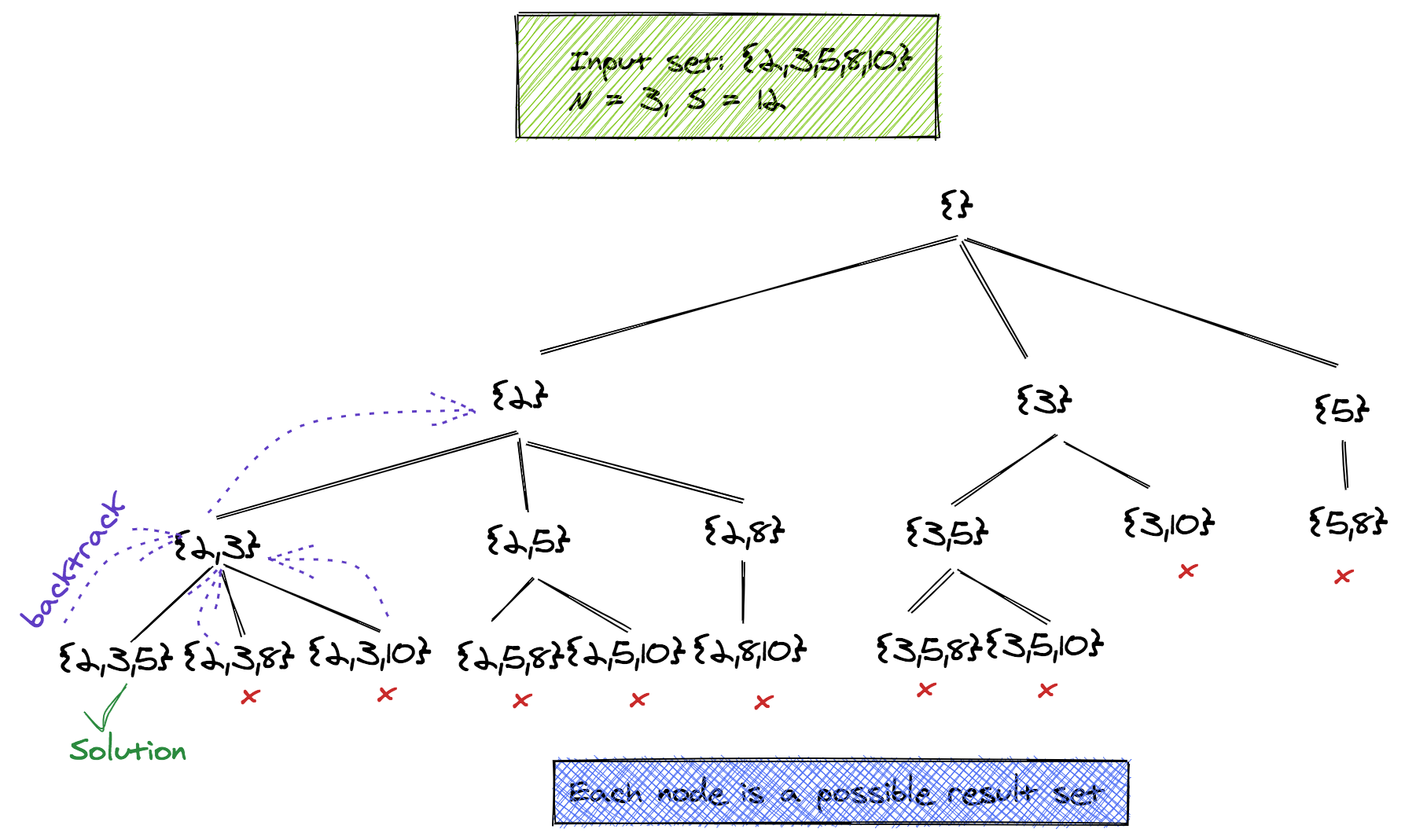기존 Recursion Tree와 동일해보이나, 근본적인 차이점으로는 역추적을 통해 선택지를 제거하고 해결책을 제시할 가능성이 있는 모든 선택지를 출력한다는 것이다.

#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;

bool compare(string a, string b)
{
    if(a.length() == b.length())
        return a<b ; // 사전순 정렬

    return a.length() < b.length();
}

void PrintSubsets(vector<string> &list)
{
    int sum = 0;
    for (auto &&i : list)
    {
        cout << i << endl;
        sum++;
    }
    cout << sum;

}
void FindSubsets(char *arr,char *temp,int i,int j,vector<string> &list)
{
    //base case
    if(arr[i] == '\0')
    {
        temp[j] = '\0';
        string s_temp(temp);
        list.push_back(temp);


        cout << endl;
        return;
    }
    //recursion case
    //Include the ith letter
    temp[j] = arr[i];
    FindSubsets(arr,temp,i+1,j+1,list);

    //Exclude the ith letter
    //OverWriting
    temp[j] = '\0';
    FindSubsets(arr,temp,i+1,j,list);
}

int main()
{
    char arr[100];
    cin >> arr;
    int n = sizeof(arr)/sizeof(char);
    char temp[n];
    vector<string> list;

    FindSubsets(arr,temp,0,0,list);
    sort(list.begin(),list.end(),compare);
    PrintSubsets(list);
}

위의 코드는 기존 Recursion에서 Backtracking의 조건이 추가되었다.

1. 배열에 문자열 셋을 기준으로 null이 나올때까지 추적한다
2. null에 도달하면 Backtracking을 수행하며 이전 출력으로 돌아간다.
3. Backtracking 상태에서 arr[i] = temp[j]에 의해 null이 overwriting 된다.
4. 1-3의 과정을 반복한다.

일련의 과정을 거쳐 수행되는데, 중요한 점은 recursion의 callstack과 그에 따른 backtracking시 절차를 잘 이해하는것 이다.

N Queens

체스 퀸을 두어 정해진 공간내에서 서로간에 간섭하지 못하도록 하는 경우의 수를 구한다.

로직을 간단히 정리해보자면

1. 정해진 보드 내에서 행 i, 열 j에 따라 퀸을 배치할곳을 찾는다.
2. 배치가능한 상태를 판별하는 CanPlace 함수를 사용한다.
3. solveQueen을 재귀호출하여 다음 행을 탐색하고 success의 반환값으로 받는다. 3-1. 재귀호출이 성공하면 true값을 반환받고 해당 index에 퀸을 고정한다. 3-2. 실패하면 false를 반환하고 backtracking을 수행한다.
4. 3번의 과정을 반복, 만약 퀸의 배치가 불가하면 backtracking의 결과를 부모에게 전달한다.

   bool solveQueen(int n, int board[][20], int i)
   {
    //base case
    if(i==n)
    {
        printBoard(n,board);
        return true;
    }
   
    // rec case
    // try to place a queen in every row
    for (int j = 0; j < n; j++)
    {
        // whether the current i,j is safe or not
        if(CanPlace(board,n,i,j))
        {
            board[i][j] = 1;
            //성공할시 다음 행 체크, 실패시 다음 열 체크 및 백트래킹 수행
            bool success = solveQueen(n,board,i+1);
            if(success)
                return true;
   
            // bactracking
            board[i][j] = 0;
        }
    }
    return false;
   }
   

   base case와 recursion case를 다룰 함수이다. 인덱스 i는 행, j를 열로 하여 각 인덱스마다 판별과정을 거쳐 퀸을 배치한다.

체스 퀸을 배치하려면 대각선 좌,우 그리고 위 아래를 판별하여야 한다. 아래는 배치할 곳의 인덱스를 기준으로 판단하는 로직이다. 행의 경우 배치된 곳 이후는 채워지지 않은 (not filled) 영역이므로 생략한다.

bool CanPlace(int board[][20], int n, int x, int y)
{
    //column
    for (int k = 0; k < x; k++)
    {
        if(board[k][y] == 1)
            return false;
    }

    //Left Diag
    int i = x;
    int j = y;
    while (i>=0 and j>=0)
    {
        if (board[i][j] == 1)
            return false;
        i--;
        j--;        
    }

    //Right Diag
    i = x;
    j = y;
    while (i>=0 and j<n)
    {
        if (board[i][j] == 1)
            return false;
        i--;
        j++;        
    }
    return true;
}

이번 문제에서는 재귀호출을 통해 부모에게 메세지를 전달하는것이 포인트라 생각한다.

bool success = solveQueen(n,board,i+1);

해당 로직을 수행하며 Parent로부터 Child까지 모두 true를 반환하면 queen의 배치가 완성되는 것이고, 이중 하나라도 false를 반환하면 backtrack을 수행하며 부모에게 전달하는 방식이다.

마치 심사위원들의 만장일치를 받아야 통과가 가능한것 처럼.. 말이다.

Grid Ways

정해진 목적지까지 이동하는 방식을 재귀로 구현하는 문제이다. 왼쪽 가장자리 위를 기준으로 목적지까지 오른쪽 또는 아래로만 움직일 수 있다.

1. i,j를 이동시켜 목적지까지 이동한다. 1-1. i==m-1, j==n-1을 만족하는 목적지에 도달하면 1을 반환한다. 1-2. 범위를 넘게되면 0을 반환하고 재귀를 이어간다.
2. 목적지까지의 반환 값 들을 모두 연산한다

아래 코드를 살펴보자.

#include<iostream>
using namespace std;
int gridWays(int i, int j,int m,int n)
{
	//base case
    //if destination arrived
    if(i == m-1 and j ==n-1)
    {
        return 1;
    }

	//if point is out of grid
    if(i >= m or j >=n)
    {
        return 0;
    }

	// f(x,y) = f(x+1,y) + f(x,y+1);
	// 나누어진 sub problem을 기준으로
    int ans = gridWays(i+1,j,m,n) + gridWays(i,j+1,m,n);
    return ans;
}

int main()
{
    int m,n;
    cin >>m>>n;
    cout << gridWays(0,0,m,n);
}

가장 핵심 부분은 재귀이다.

int  ans = gridWays(i+1,j,m,n) + gridWays(i,j+1,m,n);

gridWays를 반복 호출하며 1또는 0을 반환한다. 0을 반환하면 재귀 스택에 따라 gridWays(i,j+1,m,n) 를 수행하고 base case에서 해당 조건이 맞는지 다시 확인한다.

이러한 과정을 거쳐 반환 값을 모두 더하면 경우의 수를 출력할 수 있다.

if(i >= m or j >=n)
{
    return 0;
}

마찬가지로 grid의 위치를 벗어날 경우 0을 반환하는 즉, bounds를 지정해주어야 한다.

Sudoku

스도쿠 해결 문제이다. 해당 문제는 이전에 풀이한 queens와 닮았다 순서로 확인해보자.

1. 우선, 순회를 돌며 조건식에 맞는 값을 넣는다.
2. 다음, sudoku를 재귀호출하여 bool 값을 call stack으로 쌓는다.
3. 마지막으로, 재귀호출시 조건에 만족하는 루프가 없을경우 false를 반환하고 최초 단계로 backtracking을 수행한다.

해당 조건을 만족하도록 조건식을 작성하여야 하는데 크게 3가지 case로 나눌 수 있다.

1. column

   세로에 중복된 숫자를 금지한다.

2. row

   가로에 중복된 숫자를 금지한다.
   

3. subgrid

   subgrid 간에 중복된 숫자를 금지한다.

해당 recursion case에 맞도록 base case 또한 고려하여야 한다. base case는 누적된 bool 값을 바탕으로 column의 값이 그리드와 동일해지면 true를 반환하고 call stack을 순차적으로 부르게 한다.

---

//배치 가능여부 판단
bool CanPlaced(int board[9][9],int i,int j, int number,int n)
{
    for (int k = 0; k < 9; k++)
    {
        if(board[k][j] ==number || board[i][k] == number)
            return false;
    }

    int sx = (i/3) *3;
    int sy = (j/3) *3;

    for (int x = sx; x < sx + 3; x++)
    {
        for (int y = sy; y < sy + 3; y++)
        {
            if(board[x][y] == number)
                return false;
        }
    }
    return true;
}

// Sudoku 출력
void PrintSudoku(int board[9][9])
{
    for (int i = 0; i < 9; i++)
    {
        for (int j = 0; j < 9; j++)
        {
            cout << board[i][j] << " ";
            if((j+1) % 3 == 0)
            {
                cout << "| ";
            }
        }
        if((i+1) % 3 == 0 && i >0)
        {
            cout << endl <<" _____________________ " << endl;
        }
        cout << endl;
    }
}

// Sudoku 함수 재귀를 통한 해결 및 BackTracking 수행
bool Sudoku(int board[9][9],int i,int j,int n)
{
    if(i == n-1 && j == n-1)
    {
        cout << "done" << endl;
        PrintSudoku(board);
        return true;
    }

    if(j == n)
    {
        return Sudoku(board,i+1,0,n);
    }

    if(board[i][j] != 0)
    {
        return Sudoku(board,i,j+1,n);
    }
    for (int k = 1; k <= n; k++)
    {
        if(CanPlaced(board,i,j,k,n))
        {
            board[i][j] = k;
            bool success = Sudoku(board,i,j+1,n);
            if(success)
            {
                return true;
            }
        }
    }
    //backtracking
    board[i][j] = 0;
    return false;
    cout << "there is no answer sudoku" << endl;
}

---

위와 같이 총 3개의 기능으로 나눠 구현할 수 있다.