TA 꽈배기
rech0421k@gmail.com
TA, VR에 관심있는 지망생입니다.
[자료구조/ 알고리즘] Recursion 재귀호출 -2-
by 꽈배기
Recrusion
지난번에 한 내용을 이어서 진행하도록 하자.
Power Recursion
제곱을 재귀로 푸는 방법이다. 기존 재귀을 이용하는 방법에 최적화를 추가하였다. n의 승수만큼 2로 나누는 과정을 재귀로 호출하고 반환 시 승수가 짝수(even) 홀수(odd)에 따라 반환되는 값을 달리 한것이다.
int fastPower(int number, int n)
{
if(n ==0)
return 1;
// log2^n divide steps
int subProb = fastPower(number,n/2);
int subProbSq = subProb * subProb;
if(n & 1)
// check even or odd
return number * subProbSq;
return subProbSq;
}
int main()
{
cout << fastPower(2,10);
}
재귀 호출의 끝에 다다르면 n==0 ; return 1;을 반환하여 초기값을 1로 설정한다. subProb = 1;
이후 다음 재귀가 호출되며 짝수 또는 홀수에 따라 number * 1 => number이 반환된다. 1-1 짝수일시 subProb * subProb을 수행하여 제곱 계산 1-2 홀수일시 number * subProbSq 계산을 수행
이러한 방법을 통해 기존 재귀호출에서 시간복잡도 O(n), 공간복잡도 O(n)에서 log2^n^으로 최적화가 되었다.
Bubble Sort
버블정렬을 재귀호출으로 구현해보자. 버블정렬은 반복문으로 구현되며 재귀호출로 구현시 별다른 이득이 없다는것을 알아두자.
다른 재귀구현과 마찬가지로 순서대로 진행한다.
- base case와 recursion case로 분리한다.
- 문제를 sub problem으로 나누어 recursion 부분으로 분리한다.
- 재귀호출을 구현한다.
#include<iostream>
using namespace std;
void bubble_sort(int arr[], int n)
{
//base case
if(n == 1)
return;
for (int j = 0; j < n-1; j++)
{
if(arr[j]>arr[j+1])
swap(arr[j],arr[j+1]);
}
bubble_sort(arr,n-1);
}
int main()
{
int arr[] = {6,8,2,1,3,4};
int n = sizeof(arr)/sizeof(int);
bubble_sort_2(arr,n,0);
for (int i = 0; i < n; i++)
cout << arr[i] << " ";
}
다만 여전히 for문을 쓰는 bubble sort의 모습이 남아있다.
반복문 부분을 제거하여 아래와 같이 recursion 답게 바꿀수있다.
void bubble_sort_2(int arr[], int n,int j)
{
//base case
if(n == 1)
return;
//reduce n-1 when only recursion loops over
if(j == n-1)
{
bubble_sort_2(arr,n-1,0);
return;
}
if(arr[j]>arr[j+1])
swap(arr[j],arr[j+1]);
bubble_sort_2(arr,n,j+1);
}
재귀를 배우며 느끼는것은 while문의 조건문 제어와 상당히 비슷한 느낌을 받았다. 아니 오히려 둘의 차이점이 크지않은것 같다. 중단조건을 설정하는 재귀호출과 while이 크게 다르지 않은듯..
Number Spell
#include<iostream>
using namespace std;
#include<iostream>
using namespace std;
string spell[] = {"zero","one","two","three","four","five","six","seven","eight","nine"};
void NumberSpell(int n)
{
if(n == 0)
return;
int lastDigit = n %10;
NumberSpell(n/10);
cout << spell[lastDigit] << " , ";
}
int main()
{
int n;
cin >> n;
NumberSpell(n);
}
입력받은 정수를 각 자리수로 나누어 출력하는 재귀호출 방식이다.
int lastDigit = n %10;
NumberSpell(n/10);
cout << spell[lastDigit] << " , ";
위의 3단계로 진행되는데
- 입력받은 매개변수의 값을 나누어 나머지를 lastDigit로 가져온다.
- 매개변수의 값을 나누어 재귀호출을 수행한다.
- 모든 재귀호출이 완료되면 cout « ~ 부분을 수행한다.
이전 재귀호출과 동일하게 출력의 위치에 따라 정순 또는 역순으로 출력 될 수 있다.
Merge Sort
Recursion works in a depth first manner
병합 정렬은 분할 정복의 대표적 예시이다. 큰 문제를 작게 나누어 더이상 나눌수 없을때까지 분할하며 분할이 종료되면 병합을 수행하는 알고리즘.
아래의 3 단계로 나뉜다.
- divide
- mergesort
- merge
코드 블럭을 나누어 확인해보자.
분할 수행 코드이다. 우선 base case와 recursion case로 나누고 인덱싱을 위한 변수를 정의한다. MergeSort 재귀호출을 수행하며 분할 수행이 (s>=e 만족) 종료되면 , merge를 호출한다.
//sorting method
void MergeSort(vector<int> &arr, int s, int e)
{
//base case
//sorted or 1 array
if(s >= e)
return;
int mid = (s + e)/ 2;
// recursion case
// mergesort divide two case of array
MergeSort(arr,s,mid);
MergeSort(arr,mid+1,e);
return merge(arr,s,e);
}
int main()
{
vector<int> arr = {1,7,4,8,3,6,9};
int s = 0;
int e = arr.size()-1;
MergeSort(arr,s,e);
for (auto &&i : arr)
{
cout << i << " , ";
}
}
아래는 병합의 과정이다.
분할된 각 Sub array의 요소를 비교하며 결과를 병합한다.
한 Sub array의 요소 비교가 끝나면 남은 요소를 붙여주고 병합을 마무리한다.
// merging helper method
// 3. merge
void merge(vector<int> &arr, int s, int e)
{
int i = s;
int mid = (s+e)/2;
int j = mid+1;
vector<int> temp;
while(i <= mid and j<= e)
{
if(arr[i]<arr[j])
{
temp.push_back(arr[i]);
i++;
}
else
{
temp.push_back(arr[j]);
j++;
}
}
// sort remaining elements from part of array
while(i<=mid)
{
temp.push_back(arr[i++]);
}
while(j<=e)
{
temp.push_back(arr[j++]);
}
// copy elements from temp vector
int k =0;
for (int i = s; i < e; i++)
{
arr[i] = temp[k++];
}
return;
}
분할정복의 시간복잡도는 T(n) = 2T(n/2) + O(n) 으로 배열을 반으로 나누고 (logn) 병합하는데 (n) 선형 시간이 든다.
재귀호출에서 중요한 것은
Recursion works in a depth first manner
재귀 호출은 깊이 우선으로 작용한다는 것을 항상 기억하자.
Quick Sort
Pivot을 기준으로 두 개의 sub array로 분할하고 정렬한 다음 병합하는 방식이다. 아래의 순서를 따른다.
- Choos a pivot to divide array (especially last element)
- partition (swap based pivot) { pivot > less or pivot < greater }
- rec sort - quick sort
병합정렬의 과정이기에 Merge sort와 비슷해 보이기도 한다.
# set partition
int Partition(vector<int> &arr,int s, int e)
{
//set pivot
int pivot = arr[e];
int i = s-1;
// parition based pivot less or greater
for (int j = s; j < e; j++)
{
if(pivot > arr[j])
{
i++;
swap(arr[i],arr[j]);
}
}
// swap pivot to i+1
swap(arr[i+1],arr[e]);
return i+1;
}
#do quick sort
void QuickSort(vector<int> &arr,int s, int e)
{
//base case
if(s >= e)
return;
// rec case
int p= Partition(arr,s,e);
QuickSort(arr,s,p-1);
QuickSort(arr,p+1,e);
}
int main()
{
vector<int> arr{1,8,6,3,5,4};
int n = arr.size();
QuickSort(arr,0, n-1);
for (auto &&i : arr)
{
cout << i << " , ";
}
}
그림으로 나타내자면 위와 같다.
위의 순서처럼 pivot을 정하고 partition을 나누어 swap을 수행한다.
분할이 끝나면 병합을 시행한다.
병합 정렬과 상당히 비슷해 보인다.
Rotated Array Search
monotonic하며 모든 구간이 선형은 아닌 배열을 Pivot 없이 탐색하는 방식이다
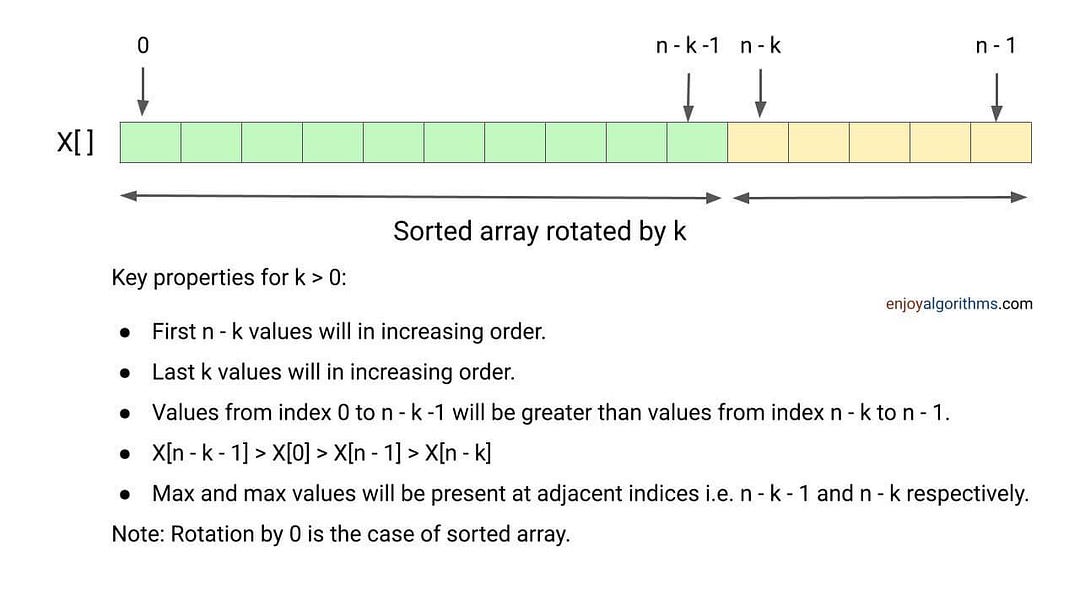총 4개의 구간을 나누어 탐색한다.
순서로는
- 배열의 case1, case2 지점을 나누어 mid로 설정한다.
- arr[mid] 를 기준으로 key의 값을 판별한다 2-1. arr[s] <= arr[mid] 일 경우 key의 값이 arr[mid]와 arr[s] 사이인지 확인한다.
- 조건에 따라 start index, end index의 값을 mid 기준으로 변경시킨다.
- 위 과정을 반복하여 값을 출력한다.
#include<iostream>
#include<vector>
using namespace std;
int RotateSearching(vector<int> & arr, int key)
{
int n = arr.size();
int s = 0;
int e = n-1;
while(s<=e)
{
int mid = (s+e)/2;
if(key == arr[mid])
{
return mid;
}
//case 1
if(arr[s] <= arr[mid])
{
if(key <= arr[mid] && key>= arr[s] )
{
e = mid-1;
}
else
{
s = mid +1;
}
}
//case 2 arr[s] >= arr[mid]
else
{
if(key >= arr[mid] and key <= arr[e])
{
s = mid+1;
}
else
{
e = mid -1;
}
}
}
return -1;
}
int main()
{
vector<int> array {4,5,6,7,0,1,2,3};
int key;
cin >> key;
cout << RotateSearching(array,key);
}