[자료구조/ 알고리즘] Recursion 재귀호출 -1-

Recrusion

Factorial

반복과는 다른 재귀 방식이다.

그중 대표적인 팩토리얼 코드를 알아보자

#include<iostream>
using namespace std;

int Factorial(int n)
{
    if(n ==0)
    {
        return 1;
    }
    //아래 부분에서 재귀가 일어난다.
    return n*Factorial(n-1);
}

int main()
{
    cout<<  Factorial(5) << edl;
}

재귀는 말그대로 자기 자신을 반복 호출하는 것이다. 반복문과는 달리 함수 call stack에 쌓여 Stack Memory를 사용한다. Stack구조에서 알 수 있듯이 마지막 호출로부터 돌아오며 재귀함수를 수행한다.

일반적으로 반복문에 비해 실행속도가 느리나, 코드가 간결한 장점이 있다.

이유는 점화식과 같이 특정 식으로 정리되기 때문이다.

Fibonacci

피보나치 Recurion Tree이다.

int Fibonacci(int n)
{
    if(n ==0 || n == 1)
    {
        return n;
    }
    return Fibonacci(n-1)+Fibonacci(n-2);
}

int main()
{
    cout<<  Fibonacci(5) << endl;
}

앞서 알아봤던대로 피보나치 또한 Stack메모리에 call stack을 쌓는다. 시간복잡도는 한번 호출에 최악의 경우 *2만큼의 연산이 반복되기에 O(2^n^)이 된다. 공간복잡도는 가장 긴 call stack을 기준으로 그 이상을 넘지 못하기에 O(n)이다.

Sorted Array Check

배열을 받아왔을때 해당 배열이 정렬되어있는지 판단하는 재귀 함수이다. isSorted 함수를 재귀시킨다 만약, 재귀 호출된 상태에서 조건을 불만족하면 false를 반환한다.

bool isSorted(int arr[],int n)
{
    //base case
    if(n==1 || n == 0)
        return true;

    //rec case arr의 인덱스 +1
    if(arr[0]< arr[1] && isSorted(arr+1,n-1))
        return true;

    return false;
}

int main()
{
    int arr[] = {1,2,3,4,5,6};
    int n = (sizeof(arr)/sizeof(int));

    cout << isSorted(arr, n) << endl;
    return 0;
}

두번째 방법으로는 인덱싱 할 변수 하나를 파라미터로 넣어주는 것이다.

bool isSortedTwo(int arr[],int i, int n)
{
    if(i == n-1)
        return true;

    if(arr[i]<arr[i+1] && isSortedTwo(arr,/*++i,*/i+1,n))
        return true;

    return false;
}

Understanding Recursion Directions

재귀함수는 재귀콜스택에 쌓이게 된다. 스택의 특성상 FILO를 유지하는데, 이 특성을 잘 기억해야 한다. 아래와 같이 기존 숫자를 늘리거나 줄이는 함수를 작성한다.

void decreasing(int n)
{
    if(n ==0)
        return;

    // call each recursion before executed
    cout<< n <<",";
    decreasing(n-1);
}

void increasing(int n)
{
    if(n ==0)
        return;

    // call after recursion executed
    increasing(n-1);
    cout<< n <<",";
}
int main()
{
    int n;
    cin >> n;
    decreasing(n);
    cout << endl;
    increasing(n);
}
10
10,9,8,7,6,5,4,3,2,1,
1,2,3,4,5,6,7,8,9,10,

집중해서 봐야할것은 출력의 순서이다. 분명 함수의 내부적인 구성은 동일한데 어떻게 출력의 순서가 반대로 나오는 것일까?

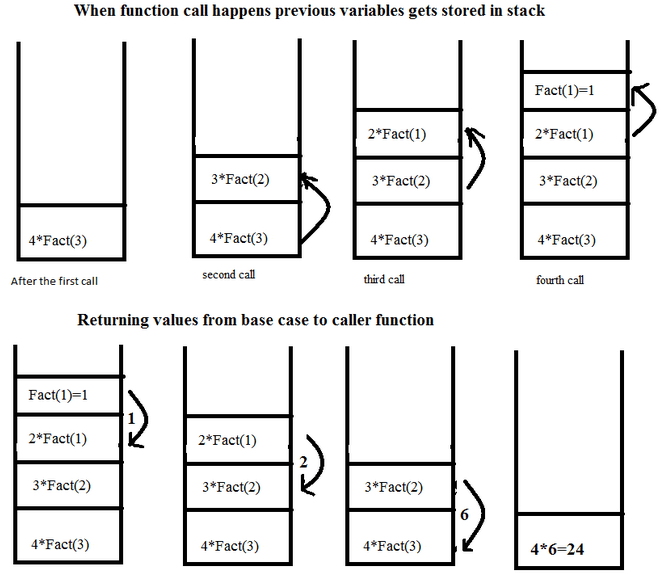
위의 그림 설명이 잘 되어있어 가져옴

10
10,9,8,7,6,5,4,3,2,1,
1,2,3,4,5,6,7,8,9,10,

재귀함수의 호출은 스택에 쌓이게되는데, cout« 출력 구문 위치에 따라 재귀 스택이 쌓일때마다 출력이 되게 할 것인지.(n=5, n=4, n=3…)

반대로 재귀스택을 모두 쌓은 후에 콜스택에 쌓인 순서대로 출력할지의 차이에 따라 해당 결과가 나오게된다. (n=1 부터 n=2 …..)

FindOccurence

배열에서 내가 원하는 숫자를 찾는 방법이다. 이를 재귀로 한번 구현해보자.

int FindOccurence(int arr[], int key, int n)
{
    //base
    if(n == 0)
        return -1;

    if (arr[0] == key)
        return 0;

    int subIndex = FindOccurence(arr+1, key, n-1);
    if(subIndex != -1)
    {
        return subIndex + 1;
    }
    return -1;
}

int main()
{
    int key;
    cin >> key;
    int arr [] = {1,2,3,4,5,6,7};

    int n = sizeof(arr)/sizeof(int);
    FindOccurence(arr,key,n);
}

생각보다 꽤 난해하였다. 배열의 탐색범위를 줄여가며 재귀가 호출된다. (subIndex) 반환값이 발생할 시 호출된 횟수에따라 인덱스 값을 더해주는 과정을 거쳐 인덱스 위치를 찾는다. 핵심은 아래 부분이다.

int subIndex = FindOccurence(arr+1, key, n-1);

1. 배열의 길이를 1씩 줄이고 인덱스 위치를 늘려가며 탐색을 한다.
2. 키값을 찾을시 0을 반환하고 subIndex +1 을 재귀만큼 반복한다.

LastOccurence

int LastOccurence(int arr[], int key, int n)
{
    if(n ==0)
        return -1;

    int subIndex = LastOccurence(arr +1, key, n-1);
    //재귀호출의 끝을 판단 0일시 -1 반환
    if(subIndex == -1)
    {
        if(arr[0] == key)
            return 0;
        else
            return -1;
    }
    else
        return subIndex + 1;
        //재귀만큼 인덱스 이동
}

위의 FindOccurence와 동일한 로직이다 하지만 Last 즉, 끝쪽 기준으로 찾는것이기 때문에 아래 로직이 재귀 호출 후 실행이 된다.

if(subIndex == -1)
    {
        if(arr[0] == key)
            return 0;
        else
            return -1;
    }
    else
        return subIndex + 1;

위 코드에서 배열 출력 순서를 바꿈으로 역순 출력을 시켰듯 여기서도 키값을 찾는 로직을 재귀후 호출되도록 하여 역순으로 찾게 만든것이다.

여러모로 재귀에 대한 이해가 있어야 확실히 이해가 될 듯 하다. 재귀호출 순서에 대한 개념을 명확히 하자.