[자료구조/ 알고리즘] Trie

Trie (prefix tree)

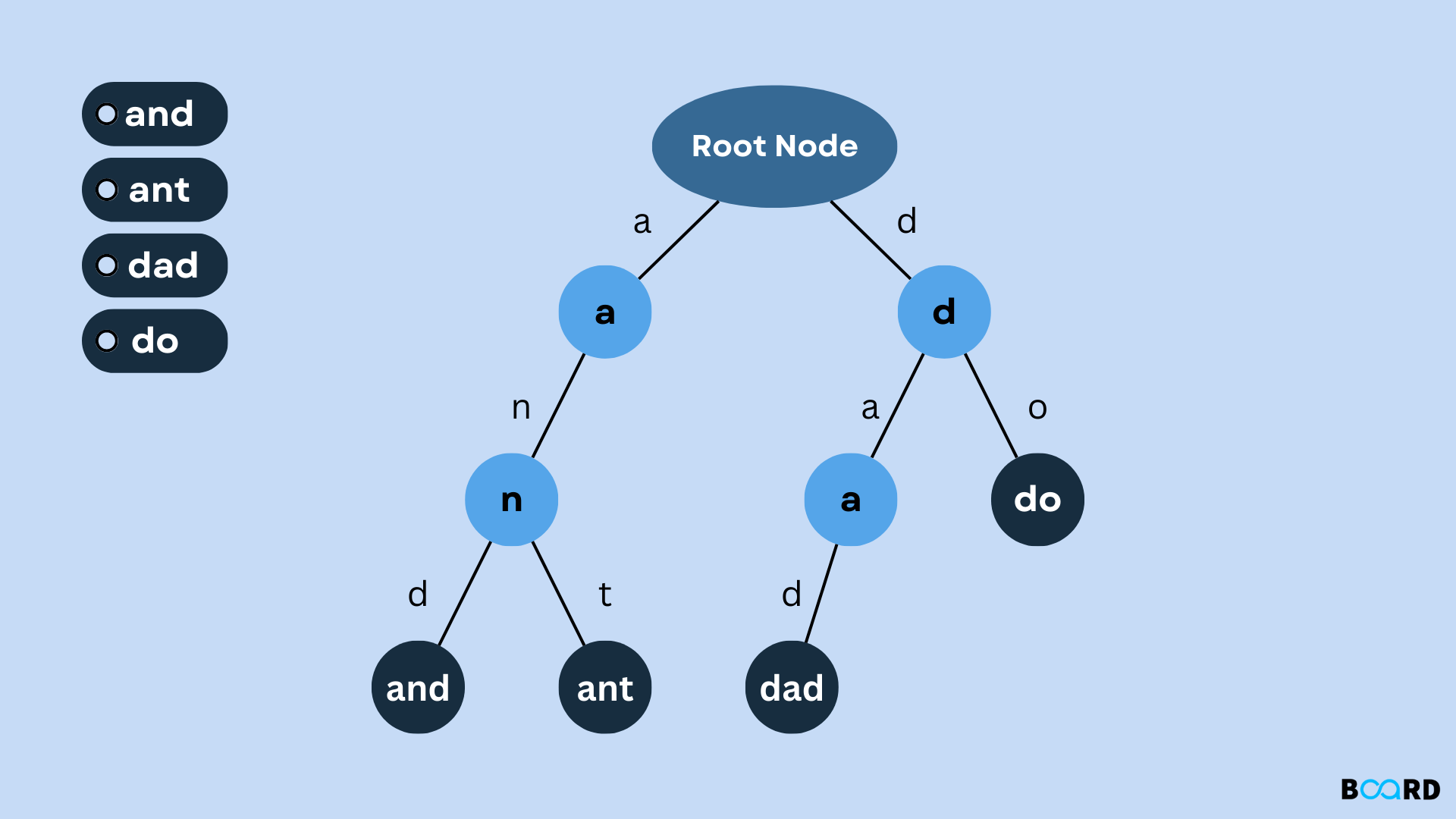
정의 및 역사

트라이(prefix tree)는 문자열 모음을 노드 형태로 저장하는 검색 데이터 구조의 일종으로, 각 노드는 문자를 나타낸다.’Trie’라는 단어는 저장된 문자열 내에서 단어나 패턴을 빠르게 검색하는 기능을 가리키는 ‘retrieval’이라는 용어에서 유래되었다.

트라이는 텍스트 데이터의 하위 문자열을 저장하고 검색하는 효율적인 방법으로 1976년 Ed McCreight에 의해 처음 소개되었습니다. 그 이후로 자동 완성 기능, 맞춤법 검사, 자연어 처리 등 많은 앱의 기본 구성 요소로 자리 잡았습니다.

장점과 단점

array나 linked list 같은 다른 데이터 구조와 비교할 때 Trie는 몇 가지 장점이 있다.

• 빠른 검색: Trie를 사용하면 저장된 문자열 내에서 특정 단어를 빠르게 검색할 수 있다.
• 효율적인 삽입: Trie에 새 단어를 삽입할 때 O(m) 시간 복잡도(입력된 단어의 길이 만큼)로 삽입할 수 있습니다.
• 공간 효율성: Trie는 각 문자를 한 번만 저장하므로 공간 효율적인 데이터 구조이다.

하지만 고려해야 할 몇 가지 단점이 있다.

• 높은 메모리 사용량: Trie 구조상 더 많은 문자열을 저장할수록 더 많은 메모리를 사용하게 되며 잠재적으로 성능 문제가 발생할 수 있다.
• 복잡성: 특히 대규모 데이터 세트의 경우 트라이를 구현하고 유지 관리하는 것이 복잡할 수 있다.
• 삽입 시간 복잡성: 큰 Trie에 새 문자열을 삽입할 때 전체 데이터 구조를 탐색해야 하기 때문에 속도가 느려질 수 있다.

Trie code

#include<iostream>
#include<string>
#include<vector>
#include<unordered_map>
using namespace std;

class TrieNode {
	char c;
public:
	bool IsEndNode;

	unordered_map<char, TrieNode*> children;
	TrieNode(char ch) {
		c = ch;
		IsEndNode = false;
	}
};

class Trie {
private:
	TrieNode* root;
public:
	Trie() {
		root = new TrieNode('\0');
	}

	void Insert(const string& word) {
		TrieNode* temp = root;
		for (char ch : word)
		{
			// 입력된 문자가 없다면
			// count는 내부에 존재하는 key 탐색
			if (!temp->children.count(ch)) {
				temp->children[ch] = new TrieNode(ch);
			}
			temp = temp->children[ch];
		}
		temp->IsEndNode = true;
	}
	bool search(const string& word) {
		TrieNode* temp = root;
		for (char ch : word)
		{
			if (!temp->children.count(ch)) {
				return false;
			}
			temp = temp->children[ch];
		}
		return true;
	}
	void deleteWord(string word) {
		deleteWord(root,word,0);
	}

private:
	bool deleteWord(TrieNode * root, string word, int idx) {
		// base case root '\0'
		if (word.size() == 1) {
			root->IsEndNode = true;
			return true;
		}
		char ch = word[idx];

		// recursion case
		if (root->children.count(ch)) {
			 auto it = root->children.find(ch);
			if (it != root->children.end()) {
				std::pair<char, TrieNode*> a = *it;
				cout << a.first << " , ";
			}
			deleteWord(root->children[ch], word, ++idx); // recursion case 는 큰 포함으로
			root->children.erase(ch);
			delete root->children[ch];
			return root->children.empty();
		}
		// 조건 불만족 return
		return false;
	}

};

int main() {
	Trie trie;
	trie.Insert("hello");
	cout << "Search word: " << trie.search("hello") << endl; // true
	trie.deleteWord("hello");
	// 우와 성공~
}

Trie 클래스 내부에는 정렬하지않는 unordered map을 사용하였다. 위와같이 내부적으로는 링크드 리스트로 구현된 것을 볼 수 있는데, 노드의 끝을 알리는 IsEndNode가 bool 타입으로 정의되어있다.

insert

문자를 입력받으면 Trie 내부에 중복되는 문자를 체크한다. 만약 존재하지 않는다면 새로운 문자를 담을 TrieNode 객체를 동적 생성하여 채인시킨다. 마지막 문자열 삽입이 끝나게 되면 IsEndNode의 값을 True로 변경시켜준다.

void Insert(const string& word) {
		TrieNode* temp = root;
		for (char ch : word)
		{
			// 입력된 문자가 없다면
			// count는 내부에 존재하는 key 탐색
			if (!temp->children.count(ch)) {
				temp->children[ch] = new TrieNode(ch);
			}
			temp = temp->children[ch];
		}
		temp->IsEndNode = true;
	}

search

입력받은 문자를 Trie 내부에서 체크하여 중복되는 문자를 출력한다. 만약 존재하지 않는다면 false를 반환하는 반면, 모든 조건이 일치하면 true를 반환한다.

bool search(const string& word) {
		TrieNode* temp = root;
		for (char ch : word)
		{
			if (!temp->children.count(ch)) {
				return false;
			}
			temp = temp->children[ch];
		}
		return true;
	}

delete

삭제의 경우 백트래킹을 사용하여, 해당되는 문자를 찾을시 재귀 호출하여 일치할때 까지 찾는다. 만약 모든 문자가 일치한다면 true를 반환하여 모두 삭제 처리하며 일치하지 않을 경우 false를 반환하여 모든 재귀 스택을 취소한다.

void deleteWord(string word) {
		deleteWord(root,word,0);
	}

private:
	bool deleteWord(TrieNode * root, string word, int idx) {
		// base case root '\0'
		if (word.size() == idx) {
			root->IsEndNode = true;
			return true;
		}
		char ch = word[idx];

		// recursion case
		if (root->children.count(ch)) {
			 auto it = root->children.find(ch);
			if (it != root->children.end()) {
				std::pair<char, TrieNode*> a = *it;
				cout << a.first << " , ";
			}
			deleteWord(root->children[ch], word, ++idx); // recursion case 는 큰 포함으로
			root->children.erase(ch);
			delete root->children[ch];
			return root->children.empty();
		}
		// 조건 불만족 return
		return false;
	}

Time complexity

다음은 트라이 데이터 구조의 각 연산에 대한 시간 복잡성에 대한 개요이다.

연산	최악의 경우 시간 복잡성	평균적인 경우
검색	O(m)	O(k)
삽입	O(m)	O(k)
삭제	O(m)	O(k)

여기서 m은 단어의 길이입니다.

• 최악의 경우: 가장 긴 문자열을 기준으로 탐색을 진행할 경우 O(m)이 된다.
• 평균값: O(k): 저장된 문자열의 평균 길이 O(k)만큼 걸린다.

Space complexity

• 최악의 경우: O(nm), 여기서 n은 트라이에 저장된 문자열의 수이고 m은 모든 문자열의 최대 길이이다.

• 평균값: O(kn), 여기서 k는 트라이에 저장된 문자열의 평균 길이이다.

Trie의 경우 대규모 문자열을 다루게 될때 공간과 시간복잡성에 문제가 생길 우려가 있다.

데이터가 많아질경우 Trie

1. 매우 큰 데이터 세트(1억 개 이상)의 경우: 대규모 데이터 세트의 경우 hash table이나 블룸 필터와 같은 다른 데이터 구조가 확장성이 더 뛰어나므로 더 적합할 수 있다.
2. 자주 업데이트해야 하는 경우: 데이터 집합이 지속적으로 변경되는 경우(예: 문자열 추가/제거)