[자료구조/ 알고리즘] Binary Search Tree

이진트리 (Binary Search Tree)

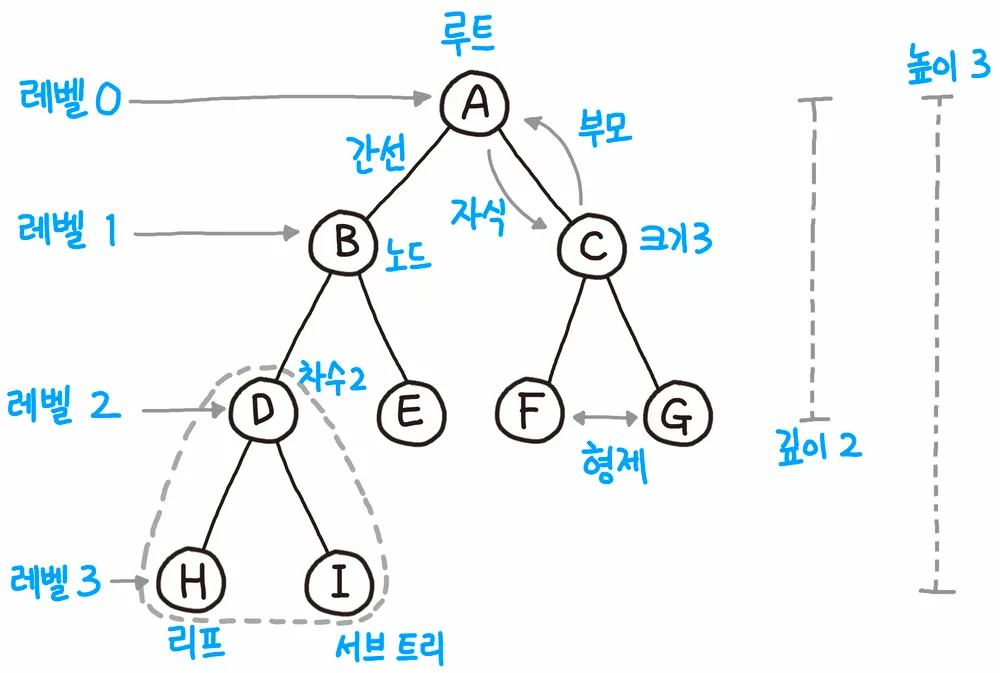root를 기준으로 왼쪽과 오른쪽 노드가 동일한 속성을 가지게 되는 트리이다.

시간 복잡도 Log n <= h <= n으로 완전 이진트리에 가까울수록 log n, 불균형시 n에 가까워진다.

Insert

Node* insert(Node * root, int key)
{
    if(root == NULL)
    {
        return new Node(key);
    }

    if(key < root->key)
    {
        root->left = insert(root->left,key);
    }
    else if (key > root->key)
    {
        root->right = insert(root->right,key);
    }

    // recursion call leaf Node as root
    // then if that Node null, Make new Node
    return root;
}

Search

bool Search(Node * root, int key)
{
    if(root == NULL)
    {
        return false;
    }
    if(root->key == key)
    {
        return true;
    }
    if(key > root->key)
    {
        Search(root->left,key);
    }
    //Don't need if cause BST
    Search(root->right,key);

    return false;
}

Deletion

이진트리의 요소 삭제로는 3가지 케이스가 있다.

1. 0 children (leaf)
2. 1 child
3. 2 children

//Deletion
/*
4. 0 children (leaf)
5. 1 child
6. 2 children
 */

Node * Deletion(Node * root, int key)
{
    if(root == NULL){
        return NULL;
    }
    else if (key < root->key){
        root->left = Deletion(root->left,key);
    }
    else if (key > root->key){
        root->right = Deletion(root->right,key);
    }
    else{
        //case 1 : 0 children (leaf)
        if((root->left == NULL) and (root->right == NULL)){
            delete root;
            root = NULL;
        }

        //case 2 : 1 child
        else if(root->left == NULL){
            Node * temp = root;
            root = root->right;
            delete temp;
        }
        else if(root->right == NULL){
            Node * temp = root;
            root = root->left;
            delete temp;
        }

        //case 3 : 2 children
        else{
            Node * temp = FindMinNode(root->right);
            // 왜 reference swap을 안해주고 데이터만 복사할까?
            root->key = temp->key;
            root->right = Deletion(root->right, temp->key);
        }
    }
    return root;
}

PrintRange

BST 노드 범위 출력

//challenge : print all elements of BST
void printRange(Node * root, int k1, int k2)
{
    if(root == NULL)
    {
        return;
    }

    if(root->key >= k1 and root->key <= k2)
    {
        //현재 노드 왼쪽 범위 출력
        printRange(root->left,k1,k2);
        cout << root->key << " ";

        //현재 노드 오른쪽 범위 출력
        printRange(root->right,k1,k2);
    }
    else if(root->key > k2) // 값을 초과할 경우 보다 작은 값으로
    {
        printRange(root->left, k1, k2);
    }
    else // 값이 미만일 경우 보다 큰 값으로
    {
        printRange(root->right, k1, k2);
    }
}

int main()
{
    Node * root = NULL;
    int arr[] = {8,3,10,1,6,14,4,7,13};

    for (int x : arr){
        root = insert(root,x);
    }
    while (root != NULL){
        cout << endl;
        printRange(root,5,13);
        cout << endl;
        int key;
        cin >> key;
        root = Deletion(root,key);

        cout<< "input :" << key << endl;
        InorderTraversal(root);
    }
    return 0;
}

모든 패스 탐색

트리에서 모든 패스를 재귀적으로 탐색해보자.

void RootToLeaf(Node * root, vector<int> &path)
{
    if(root == NULL){
        return;
    }
    if(root->left == NULL and root->right == NULL){
        for (int node:path){
            cout << node << " -> ";
        }
        cout << root->key << "  ";
        cout << endl;
        return;
    }
    path.push_back(root->key);
    RootToLeaf(root->left,path);
    RootToLeaf(root->right,path);

    path.pop_back();
    return; //backtracking을 위한 return
}