[자료구조/ 알고리즘] Binary tree

Tree

순서가 정해진 트리 형태의 계층적 자료구조이다.

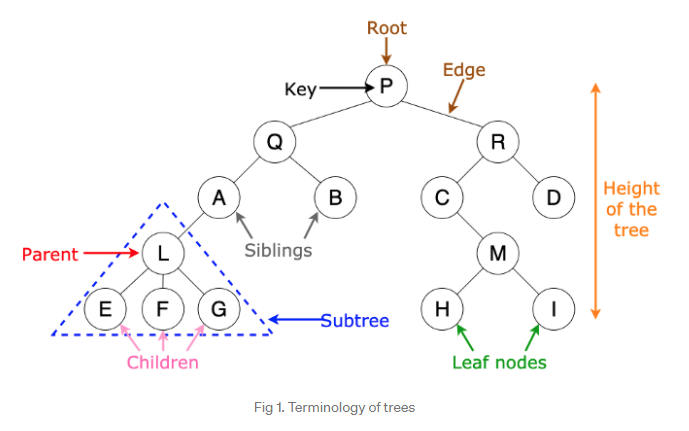
• depth : 루트 노드 깊이 0부터 특정 노드까지의 길이 이다.
• level : 루트 노드에서 자신까지 가는 경로의 길이 더하기 1이다.
• height : 노드와 단말 노드 사이의 경로의 최대 길이이다.
• size : 자기 자신 및 모든 자손 노드의 수이다.

PreOrder

//Root - Left - Right
void PreorderSearching(Node * n)
{
    if(n == NULL)
    {
        // cout << -1 << " - ";
        return;
    }

    cout << n->data << " - ";

    PreorderSearching(n->left);
    PreorderSearching(n->right);
}

부모 -> 왼쪽 -> 오른쪽 순서대로 탐색하는 방식이다.

Inorder

//Left - Root - Right
void InorderTraversal(Node * n)
{
    if(n == NULL)
    {
        return;
    }

    InorderTraversal(n->left);
    cout << n->data << " - ";
    InorderTraversal(n->right);

}

왼쪽 -> 부모 -> 오른쪽 순서대로 탐색하는 방식이다.

PostOrder

//Left - Right - Root
void PostorderTraversal(Node * n)
{
    if(n == NULL)
    {
        return;
    }

    PostorderTraversal(n->left);
    PostorderTraversal(n->right);
    cout << n->data << " - ";

}

왼쪽 -> 오른쪽 -> 부모 순서대로 탐색하는 방식이다.

BFS

void BFS(Node* root)
{
    queue<Node*> q;
    q.push(root);
    q.push(NULL);

    while (!q.empty())
    {
        Node* temp = q.front();
        if(temp == NULL)
        {
            //줄바꿈
            q.pop();
            cout<< endl;
            // q에 새로운 줄바꿈 추가
            if(!q.empty())
            {
                q.push(NULL);
            }
        }
        else
        {
            q.pop();
            cout << temp->data << " ";
            if(temp->left != NULL)
            {
                q.push(temp->left);
            }
            if(temp->right != NULL)
            {
                q.push(temp->right);
            }
        }
    }
    return;
}

Node* BFSBuilder()
{
    int d;
    cin >> d;

    Node* root = new Node(d);

    queue<Node*> q;
    q.push(root);

    while (!q.empty())
    {
        Node* current = q.front();
        q.pop();

        //offer child data
        int c1, c2;
        cin >> c1 >> c2;
        if(c1 != -1)
        {
            current->left = new Node(c1);
            q.push(current->left);
        }
        if(c2 != -1)
        {
            current->right = new Node(c2);
            q.push(current->right);
        }
    }
    return root;
}

Diameter

가장 먼 지점을 연결했을때 거리를 나타낸다.

int Height(Node* root)
{
    if(root == NULL)
    {
        return 0;
    }

    int h1 = Height(root->left);
    int h2 = Height(root->right);

    return 1+ max(h1,h2);
}
int Diameter(Node* root)
{
    if (root == NULL)
    {
        return 0;
    }


    int D1 = Height(root->left) + Height(root->right);
    int D2 = Diameter(root->left);
    int D3 = Diameter(root->right);
    int diameter = max(D1,max(D2,D3));

    return diameter;
}

Diameter Optimize

최적화를 적용해보자. 높이를 계산할 때 부분 서브 트리의 diameter 를 반환받을 수 있다.

그렇기에 이전 height를 구할때 수행되던 연산을 줄여 최적화 할 수 있다.

class HDPair
{
public:
    int height;
    int diameter;
};

HDPair opt_Diameter(Node* root)
{
    HDPair pair;
    if(root == NULL)
    {
        pair.diameter = pair.height = 0;
        return pair;
    }

    HDPair left = opt_Diameter(root->left);
    HDPair right = opt_Diameter(root->right);

    //optimized O(N) -> O(1)
    //when calc height, also we can return particular subtrees diameter
    pair.height = max(left.height,right.height)+1;
    int D1 = left.height + right.height;
    int D2 = left.diameter;
    int D3 = right.diameter;

    pair.diameter = max(D1,max(D2,D3));
    return pair;
}